
【題目】某企業生成一種節能產品,投放市場供不應求.若該企業每月的產量保持在一定的范圍,每套產品的生產成本不高于50萬元,每套產品的售價不低于120萬元.已知這種產品的月產量x(套)與每套的售價y1(萬元)之間滿足關系式y1=190﹣2x.月產量x(套)與生成總成本y2(萬元)存在如圖所示的函數關系.
(1)直接寫出y2(2)與x之間的函數關系式;
(2)求月產量x的取值范圍;
(3)當月產量x(套)為多少時,這種產品的利潤W(萬元)最大?最大利潤是多少?
【答案】
(1)
解:設y2與x的函數關系式為y2=kx+b,
![]() ,得
,得 ![]() ,
,
∴y2與x之間的函數關系式是y2=30x+500
(2)
解:由題意可得,
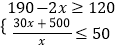 ,
,
解得,25≤x≤35,
即月產量x的取值范圍是25≤x≤35
(3)
解:由題意可得,
W=x[190﹣2x﹣ ![]() ]=﹣2(x﹣40)2+2700,
]=﹣2(x﹣40)2+2700,
∵25≤x≤35,
∴x=35時,W取得最大值,此時W=2650,
即當月產量x(套)為35套時,這種產品的利潤W(萬元)最大,最大利潤是2650萬元.
【解析】(1)根據題意可以設出y2與x之間的函數關系式,然后根據圖象中的數據即可求得函數的解析式;(2)根據題意可以列出相應的不等式組,從而可以求得x的取值范圍;(3)根據題意可以得到W與x函數關系式,然后化為頂點式,再根據x的取值范圍,即可求得W的最大值.


 仁愛英語同步練習冊系列答案
仁愛英語同步練習冊系列答案 學習實踐園地系列答案
學習實踐園地系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,∠BAC=54°,以AB為直徑的⊙O分別交AC,BC于點D,E,過點B作⊙O的切線,交AC的延長線于點F. 
(1)求證:BE=CE;
(2)求∠CBF的度數;
(3)若AB=6,求 ![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,反比例函數y= ![]() (x>0)的圖象經過矩形OABC對角線的交點M,分別與AB、BC相交于點D、E.,則下列結論正確的是(將正確的結論填在橫線上).
(x>0)的圖象經過矩形OABC對角線的交點M,分別與AB、BC相交于點D、E.,則下列結論正確的是(將正確的結論填在橫線上).
①s△OEB=s△ODB , ②BD=4AD,③連接MD,S△ODM=2S△OCE , ④連接ED,則△BED∽△BCA.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y1=kx+b的圖象與反比例函數y2= ![]() 的圖象相交于點A(2,3)和點B,與x軸相交于點C(8,0).
的圖象相交于點A(2,3)和點B,與x軸相交于點C(8,0). 
(1)求這兩個函數的解析式;
(2)當x取何值時,y1>y2 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC在平面直角坐標系xOy中的位置如圖所示.

(1)作△ABC關于點C成中心對稱的△A1B1C1.
(2)將△A1B1C1向右平移4個單位,作出平移后的△A2B2C2.
(3)在x軸上求作一點P,使PA1+PC2的值最小,并寫出點P的坐標(不寫解答過程,直接寫出結果)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,點A、D、B、E在同一直線上,AC=EF,AD=BE,∠A=∠E,
(1)求證:△ABC≌△EDF;
(2)當∠CHD=120°,猜想△HDB的形狀,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據2008~2012年杭州市實現地區生產總值(簡稱GDP,單位:億元)統計圖所提供的信息,下列判斷正確的是( ) 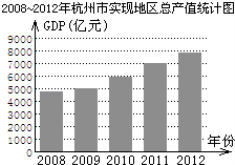
A.2010~2012年杭州市每年GDP增長率相同
B.2012年杭州市的GDP比2008年翻一番
C.2010年杭州市的GDP未達到5500億元
D.2008~2012年杭州市的GDP逐年增長
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義符號min{a,b}的含義為:當a≥b時min{a,b}=b;當a<b時min{a,b}=a.如:min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.則min{﹣x2+1,﹣x}的最大值是( )
A.![]()
B.![]()
C.1
D.0
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com