
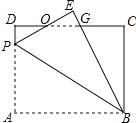
【題目】如圖,矩形ABCD中,AB=4,BC=3,P為AD上一點(diǎn),將△ABP沿BP翻折至△EBP,PE與CD相交于點(diǎn)O,且OE=OD,則AP的長為_____.

【答案】2.4
【解析】
由折疊的性質(zhì)得出EP=AP,∠E=∠A=90°,BE=AB=4,由ASA證明△ODP≌△OEG,得出OP=OG,PD=GE,設(shè)AP=EP=x,則PD=GE=3﹣x,DG=x,求出CG、BG,根據(jù)勾股定理得出方程,解方程即可.
解:如圖所示:∵四邊形ABCD是矩形,
∴∠D=∠A=∠C=90°,AD=BC=3,CD=AB=4,
根據(jù)題意得:△ABP≌△EBP,
∴EP=AP,∠E=∠A=90°,BE=AB=4,
在△ODP和△OEG中,
 ,
,
∴△ODP≌△OEG(ASA),
∴OP=OG,PD=GE,
∴DG=EP,
設(shè)AP=EP=x,則PD=GE=3﹣x,DG=x,
∴CG=4﹣x,BG=4﹣(3﹣x)=1+x,
根據(jù)勾股定理得:BC2+CG2=BG2,
即32+(4﹣x)2=(x+1)2,
解得:x=2.4,
∴AP=2.4;
故答案為:2.4.


 互動課堂系列答案
互動課堂系列答案 激活思維智能訓(xùn)練課時(shí)導(dǎo)學(xué)練系列答案
激活思維智能訓(xùn)練課時(shí)導(dǎo)學(xué)練系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】小明為了了解氣溫對用電量的影響,對去年自己家的每月用電量和當(dāng)?shù)貧鉁剡M(jìn)行了統(tǒng)計(jì).去年當(dāng)?shù)孛吭碌钠骄鶜鉁厝鐖D1,小明家去年月用電量如圖2.

根據(jù)統(tǒng)計(jì)圖,回答下面的問題:
(1)當(dāng)?shù)厝ツ暝缕骄鶜鉁氐淖罡咧怠⒆畹椭蹈鳛槎嗌伲肯鄳?yīng)月份的用電量各是多少?
(2)請簡單描述月用電量與氣溫之間的關(guān)系;
(3)假設(shè)去年小明家用電量是所在社區(qū)家庭用電量的中位數(shù),據(jù)此他能否預(yù)測今年該社區(qū)的年用電量?請簡要說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】二次函數(shù)![]() 的部分圖象如圖,圖象過點(diǎn)(﹣1,0),對稱軸為直線
的部分圖象如圖,圖象過點(diǎn)(﹣1,0),對稱軸為直線![]() ,下列結(jié)論:①
,下列結(jié)論:①![]() ;②
;②![]() ;③
;③![]() ;④當(dāng)
;④當(dāng)![]() 時(shí),
時(shí), ![]() 隨
隨![]() 的增大而增大.其中正確的結(jié)論有( )
的增大而增大.其中正確的結(jié)論有( )

A. 1個(gè) B. 2個(gè) C. 3個(gè) D. 4個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某水果店11月份購進(jìn)甲、乙兩種水果共花費(fèi)1700元,其中甲種水果8元/千克,乙種水果18元/千克.12月份,這兩種水果的進(jìn)價(jià)上調(diào)為:甲種水果10元/千克,乙種水果20元/千克.
(1)若該店12月份購進(jìn)這兩種水果的數(shù)量與11月份都相同,將多支付貨款300元,求該店11月份購進(jìn)甲、乙兩種水果分別是多少千克?
(2)若12月份將這兩種水果進(jìn)貨總量減少到120千克,設(shè)購進(jìn)甲種水果a千克,需要支付的貨款為w元,求w與a的函數(shù)關(guān)系式;
(3)在(2)的條件下,若甲種水果不超過90千克,則12月份該店需要支付這兩種水果的貨款最少應(yīng)是多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() .動點(diǎn)
.動點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā),按
出發(fā),按![]() 的路徑運(yùn)動,且速度為
的路徑運(yùn)動,且速度為![]() ,設(shè)出發(fā)時(shí)間為
,設(shè)出發(fā)時(shí)間為![]() .
.

(1)求![]() 的長.
的長.
(2)當(dāng)![]() 時(shí),求證:
時(shí),求證:![]() .
.
(3)當(dāng)點(diǎn)![]() 在
在![]() 邊上運(yùn)動時(shí),若
邊上運(yùn)動時(shí),若![]() 是以
是以![]() 為腰的等腰三角形,求出所有滿足條件的
為腰的等腰三角形,求出所有滿足條件的![]() 的值.
的值.
(4)在整個(gè)運(yùn)動過程中,若![]() (
(![]() 為正整數(shù)),則滿足條件的
為正整數(shù)),則滿足條件的![]() 的值有________個(gè).
的值有________個(gè).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,把長方形紙片ABCD折疊,使頂點(diǎn)A與頂點(diǎn)C重合在一起,EF為折痕.若AB=3,BC=9.點(diǎn)D對應(yīng)點(diǎn)是G.

(1)求BE長;
(2)求EF長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=4,O為AC中點(diǎn),若點(diǎn)D在直線BC上運(yùn)動,連接OE,則在點(diǎn)D運(yùn)動過程中,線段OE的最小值是為( )

A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分線,點(diǎn)O在AB上,⊙O經(jīng)過B,D兩點(diǎn),交BC于點(diǎn)E.
(1)求證:AC是⊙O的切線;
(2)若AB=6,sin∠BAC=![]() ,求BE的長.
,求BE的長.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知△ABC是等腰直角三角形,∠BAC=90°,BE是∠ABC的平分線,DE⊥BC,垂足為D.

(1)請你寫出圖中所有的等腰三角形;
(2)請你判斷AD與BE垂直嗎?并說明理由.
(3)如果BC=10,求AB+AE的長.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com