Question

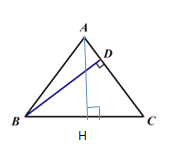
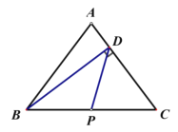
【題目】如圖，在中，，，交于點.動點從點出發，按的路徑運動，且速度為，設出發時間為.

（1）求的長.

（2）當時，求證：.

（3）當點在邊上運動時，若是以為腰的等腰三角形，求出所有滿足條件的的值.

（4）在整個運動過程中，若（為正整數），則滿足條件的的值有________個.

Answer 1

【答案】(1);(2)見解析;(3)見解析;(4) 無數個.

【解析】

(1)利用等腰三角形的性質和勾股定理求三角形的高AH的長度，然后根據三角形的面積法求BD的長；（2）根據題意計算出AP=AD，然后利用SAS定理證明，從而利用全等三角形的性質進行證明；（3）分情況討論當CP=CD或CP=DP時，分別求此時CP的長度，從而求t的值；（4）根據題意求出，從而確定三角形面積的值有無數個，所以t的值有無數個.

（1）解：過點作交于點.

∵

∴

∴

∵

∴

（2）當時，

此時點在邊上，且

由（1）可得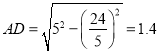

∴

∵.

∴

∴

∴

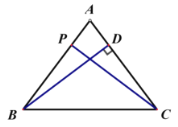
（3）當點img src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/27/10/c88d1317/SYS202011271015219315411118_DA/SYS202011271015219315411118_DA.016.png" width="15" height="16" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />在邊上運動時，

①當時，是等腰三角形

∵

∴

∴

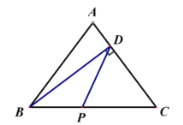
②當時，是等腰三角形

∵

∴

∵，

∴

∴

∴為中點

∴

∴

∴

∴當是以為腰的等腰三角形時，的值為6.2或6.5.

（4）由（1）得知

∴

又∵n為正整數，

∴的值有無數個

∴滿足條件的的值無數個.