
【題目】如圖,在平面直角坐標系xOy中,一次函數y=k1x+b的圖象與x軸交于點A(-3,0),與y軸交于點B,且與正比例函數y=kx的圖象交點為C(3,4).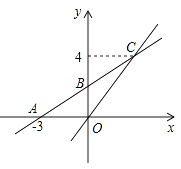
(1)求正比例函數與一次函數的關系式;
(2)若點D在第二象限,△DAB是以AB為直角邊的等腰直角三角形,請求出點D的坐標;
(3)在x軸上是否存在一點E使△BCE周長最小,若存在,求出點E的坐標
(4)在x軸上求一點P使△POC為等腰三角形,請直接寫出所有符合條件的點P的坐標.
【答案】
(1)解:∵一次函數y=k1x+b過點A(-3,0); C(3,4)
∴ ![]() 解得:
解得: 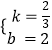
∴一次函數關系式為y= ![]() x+2
x+2
∵正比例函數y=kx的圖象過點為C(3,4)
∴4=-3k2
∴k2= ![]() 正比例函數:y=
正比例函數:y= ![]() x
x
(2)解:如圖所示,作D1M⊥X軸于M點,作D2N⊥Y軸于N,在等腰△AD1B中,
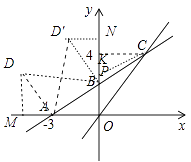
A D1=AB ; ∠D1AB=90° ∠D1DA=∠AOB=90°
∴∠D1AM+∠BAO=90° 又∵∠ABO+∠BAO=90°
∴∠D1AM =∠BAO
在△D1DA與△ OAB中
∠D1AM =∠BAO(已證)
∠D1MA=∠AOB(已證)
A D1=AB (已證)
∴△D1MA≌△OAB(AAS)
∴D1 M=OA=3;AM=BO=2 ∴OM=5
∵D1在第二象限,∴D1(-5,3)
同理證:△D2NB≌△BOA(AAS) ∴D2(-2,5)
(3)解:存在;作C關于X軸對稱點C1,連接BC1,交X軸于E,此時△BCE周長最小。
∵ ![]() ∴
∴ ![]()
∴BC1的解析式為:y=-2x+2
令y=0,得0=-2x+2, x=1
∴E點的坐標為(1,0)
(4)解:P (5,0)
P (-5,0)
P (6, 0)
P ( ![]() ,0)
,0)
【解析】(4)①當OC是腰,O是頂角的頂點時,OP=OC,則點P的坐標為(5,0)或(-5,0);
②當OC是腰,C是頂角的頂點時,CP=CP,則點P與點O關于x=3對稱,則點P的坐標為(6,0);
③當OC是底邊時,設點P的坐標為(a,0),則(a-3)2+42=a2,解得a=![]() ,則點P的坐標為(
,則點P的坐標為(![]() ,0).
,0).
綜上可知,點P的坐標(5,0)或(-5,0)或(6,0)或(![]() ,0).
,0).
【考點精析】解答此題的關鍵在于理解一次函數的性質的相關知識,掌握一般地,一次函數y=kx+b有下列性質:(1)當k>0時,y隨x的增大而增大(2)當k<0時,y隨x的增大而減小,以及對一次函數的圖象和性質的理解,了解一次函數是直線,圖像經過仨象限;正比例函數更簡單,經過原點一直線;兩個系數k與b,作用之大莫小看,k是斜率定夾角,b與Y軸來相見,k為正來右上斜,x增減y增減;k為負來左下展,變化規律正相反;k的絕對值越大,線離橫軸就越遠.


 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案科目:初中數學 來源: 題型:
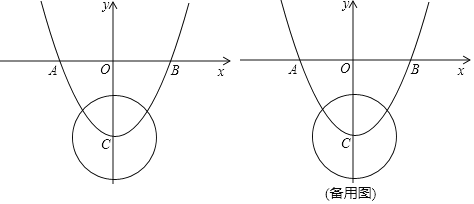
【題目】如圖,已知二次函數![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() 兩點與
兩點與![]() 軸交于點
軸交于點![]() ,⊙
,⊙![]() 的半徑為
的半徑為![]() 為⊙
為⊙![]() 上一動點.
上一動點.
(1)點![]() 的坐標分別為
的坐標分別為![]() ( ),
( ),![]() ( );
( );
(2)是否存在點![]() ,使得
,使得![]() 為直角三角形?若存在,求出點
為直角三角形?若存在,求出點![]() 的坐標;若不存在,請說明理由;
的坐標;若不存在,請說明理由;
(3)連接![]() ,若
,若![]() 為
為![]() 的中點,連接
的中點,連接![]() ,則
,則![]() 的最大值= .
的最大值= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了解全校學生對新聞、體育、動畫、娛樂、戲曲五類電視節目的喜愛情況,隨機選取該校部分學生進行調查,要求每名學生從中只選一類最喜愛的電視節目.以下是根據調查結果繪制的統計圖表的一部分.
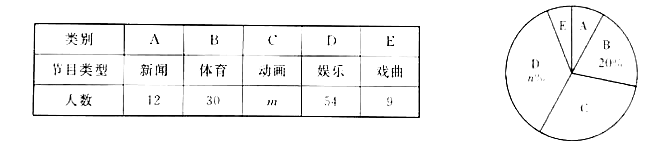
根據以上信息,解答下列問題:
(1)被調查的學生中,最喜愛體育節目的有 人,這些學生數占被調查總人數的百分比為 %;
(2)被調查學生的總數為 人,統計表中![]() 的值為 ,統計圖中
的值為 ,統計圖中![]() 的值為 ;
的值為 ;
(3)在統計圖中,![]() 類所對應扇形圓心角的度數為 ;
類所對應扇形圓心角的度數為 ;
(4)該校共有2000名學生,根據調查結果,估計該校最喜愛欣慰節目的學生數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,四邊形![]() 的頂點
的頂點![]() 是坐標原點,點
是坐標原點,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 分別為四邊形
分別為四邊形![]() 邊上的動點,動點
邊上的動點,動點![]() 從點
從點![]() 開始,以每秒1個單位長度的速度沿
開始,以每秒1個單位長度的速度沿![]() 路線向中點
路線向中點![]() 勻速運動,動點
勻速運動,動點![]() 從
從![]() 點開始,以每秒兩個單位長度的速度沿
點開始,以每秒兩個單位長度的速度沿![]() 路線向終點
路線向終點![]() 勻速運動,點
勻速運動,點![]() 同時從
同時從![]() 點出發,當其中一點到達終點后,另一點也隨之停止運動。設動點運動的時間
點出發,當其中一點到達終點后,另一點也隨之停止運動。設動點運動的時間![]() 秒(
秒(![]() ),
),![]() 的面積為
的面積為![]() .
.
(1)填空:![]() 的長是 ,
的長是 ,![]() 的長是 ;
的長是 ;
(2)當![]() 時,求
時,求![]() 的值;
的值;
(3)當![]() 時,設點
時,設點![]() 的縱坐標為
的縱坐標為![]() ,求
,求![]() 與
與![]() 的函數關系式;
的函數關系式;
(4)若![]() ,請直接寫出此時
,請直接寫出此時![]() 的值.
的值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com