
已知雙曲線 與直線
與直線 相交于A、B兩點.第一象限上的點M(
相交于A、B兩點.第一象限上的點M( )在雙曲線
)在雙曲線 上(在A點左側).過點B作BD∥y軸交x軸于點D.過N(0,-n)作NC∥x軸交雙曲線
上(在A點左側).過點B作BD∥y軸交x軸于點D.過N(0,-n)作NC∥x軸交雙曲線 于點E,交BD于點C.
于點E,交BD于點C.

(1)若點D坐標是(-8,0),求A、B兩點坐標及 的值;
的值;
(2)若B是CD的中點,四邊形OBCE的面積為4,求此時M點的坐標;
(3)在(2)的條件下,設直線AM分別與x軸、y軸相交于點P、Q兩點,求MA:PQ的值.
【解析】(1)根據B點的橫坐標為-8,代入y=1/4x中,得y=-2,得出B點的坐標,即可得出A點的坐標,再根據k=xy求出即可;
(2)根據S矩形DCNO=2mn=2k,S△DBO=  mn=
mn=
 k,S△OEN=
k,S△OEN=  mn=
mn=
 2k,即可得出k的值,
2k,即可得出k的值,
(3)首先求出直線MA解析式,再利用相似或勾股定理解得
(1)B(-8,-2).而A、B兩點關于原點對稱,∴A(8,2).
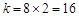 .……………………………………………2分
.……………………………………………2分
(2)∵N(0,-n),B是CD的中點,A、B、M、E四點均在雙曲線上,
∴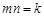 ,B(-2m,-
,B(-2m,-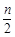 ),C(-2m,-n),E(-m,-n).
),C(-2m,-n),E(-m,-n).
S矩形DCNO ,S△DBO=
,S△DBO=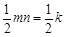 ,S△OEN =
,S△OEN =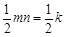 ,
,
∴S四邊形OBCE= S矩形DCNO-S△DBO- S△OEN=k.∴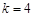 . …………4分
. …………4分
由直線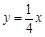 及雙曲線
及雙曲線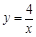 ,得A(4,1),B(-4,-1),
,得A(4,1),B(-4,-1),
∴M(2,2).……………………………………………………6分
(3)求出直線MA解析式為: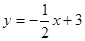 ,所以P(-6,0),Q(0,3)
,所以P(-6,0),Q(0,3)
利用相似或勾股定理得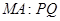 =
=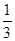 ………………………… 10分
………………………… 10分


科目:初中數學 來源:2012屆江蘇泰興市黃橋初級中學八年級下期中數學試卷(帶解析) 題型:解答題
已知雙曲線 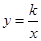 與直線
與直線 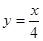 相交于A、B兩點.第一象限上的點M(m,n)(在A點左側)是雙曲線
相交于A、B兩點.第一象限上的點M(m,n)(在A點左側)是雙曲線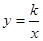 上的動點.過點B作BD∥y軸交x軸于點D.過N(0,-n)作NC∥x軸交雙曲線
上的動點.過點B作BD∥y軸交x軸于點D.過N(0,-n)作NC∥x軸交雙曲線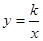 于點E,交BD于點C.
于點E,交BD于點C.
【小題1】若點D坐標是(-8,0),求A、B兩點坐標及k的值.
【小題2】若B是CD的中點,四邊形OBCE的面積為4,求直線CM的解析式.
【小題3】在(2)的條件下,若P為x軸上一點,是否存在△OMP為等腰三角形?若存在,寫出P點坐 標;若不存在,說明理由。
標;若不存在,說明理由。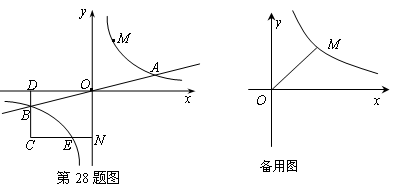
查看答案和解析>>
科目:初中數學 來源:2008年初中畢業升學考試(江蘇南通卷)數學(帶解析) 題型:解答題
已知雙曲線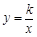 與直線
與直線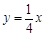 相交于A、B兩點.第一象限上的點M(m,n)(在A點左側)是雙曲線
相交于A、B兩點.第一象限上的點M(m,n)(在A點左側)是雙曲線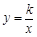 上的動點.過點B作BD∥y軸交x軸于點D.過N(0,-n)作NC∥x軸交雙曲線
上的動點.過點B作BD∥y軸交x軸于點D.過N(0,-n)作NC∥x軸交雙曲線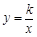 于點E,交BD于點C.
于點E,交BD于點C.
(1)若點D坐標是(-8,0),求A、B兩點坐標及k的值.
(2)若B是CD的中點,四邊形OBCE的面積為4,求直線CM的解析式.
(3)設直線AM、BM分別與y軸相交于P、Q兩點,且MA=pMP,MB=qMQ,求p-q的值.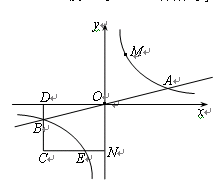
查看答案和解析>>
科目:初中數學 來源:2013年初中數學單元提優測試卷-反比例函數與一次函數的圖像(帶解析) 題型:解答題
已知雙曲線 與直線
與直線 相交于A、B兩點.第一象限上的點M(m,n)(在A點左側)是雙曲線
相交于A、B兩點.第一象限上的點M(m,n)(在A點左側)是雙曲線 上的動點.過點B作BD∥y軸交x軸于點D.過N(0,﹣n)作NC∥x軸交雙曲線
上的動點.過點B作BD∥y軸交x軸于點D.過N(0,﹣n)作NC∥x軸交雙曲線 于點E,交BD于點C.
于點E,交BD于點C.
(1)若點D坐標是(﹣8,0),求A、B兩點坐標及k的值.
(2)若B是CD的中點,四邊形OBCE的面積為4,求直線CM的解析式.
查看答案和解析>>
科目:初中數學 來源:2008年初中畢業升學考試(江蘇南通卷)數學(解析版) 題型:解答題
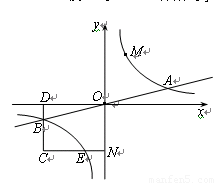
已知雙曲線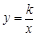 與直線
與直線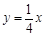 相交于A、B兩點.第一象限上的點M(m,n)(在A點左側)是雙曲線
相交于A、B兩點.第一象限上的點M(m,n)(在A點左側)是雙曲線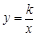 上的動點.過點B作BD∥y軸交x軸于點D.過N(0,-n)作NC∥x軸交雙曲線
上的動點.過點B作BD∥y軸交x軸于點D.過N(0,-n)作NC∥x軸交雙曲線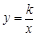 于點E,交BD于點C.
于點E,交BD于點C.
(1)若點D坐標是(-8,0),求A、B兩點坐標及k的值.
(2)若B是CD的中點,四邊形OBCE的面積為4,求直線CM的解析式.
(3)設直線AM、BM分別與y軸相交于P、Q兩點,且MA=pMP,MB=qMQ,求p-q的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com