
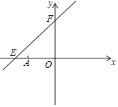
【題目】如圖,直線y=kx+6與x軸、y軸分別相交于點E、F,點E的坐標為(-8,0),點A的坐標為(-6,0),點P是直線EF上的一個動點.
(1)求k的值;
(2)點P在第二象限內的直線EF上的運動過程中,寫出△OPA的面積S與x的函整表達式,并寫出自變量x的取值范圍;
(3)探究,當點P在直線EF上運動到時,△OPA的面積可能是15嗎,若能,請求出點P的坐標;若不能,說明理由.
【答案】(1)![]() ;(2)S=
;(2)S=![]() x+18,-8<x<0;(3)(
x+18,-8<x<0;(3)(![]() ,5)或(
,5)或(![]() ,-5)
,-5)
【解析】
(1)根據待定系數法,可得k值;(2)根據點在直線上,可得P點坐標,根據三角形的面積公式,可得函數解析式;再根據P(x,y)是第二象限內的直線上,可得自變量的取值范圍;(3)根據點在直線上,可得點Q坐標(x,![]() x+6),根據三角形的面積,可得關于x的方程,根據解方程,可得x的值,根據自變量與函數值的對應關系,可得Q點坐標.
x+6),根據三角形的面積,可得關于x的方程,根據解方程,可得x的值,根據自變量與函數值的對應關系,可得Q點坐標.
解:(1)把E(-8,0)代入直線y=kx+6中,得0=-8k+6,
解得:k=![]() ;
;
(2)P在第二象限內的直線EF上的運動:y=![]() x+6,
x+6,
設P坐標是:(x,![]() x+6)
x+6)
S△OPA=![]() ×|OA|×(
×|OA|×(![]() x+6)
x+6)
=![]() ×6×(
×6×(![]() x+6)
x+6)
=![]() x+18,
x+18,
P在第二象限內的直線EF上的運動,得
-8<x<0.
∴△OPA的面積S與x的函數關系式為S=![]() x+18,
x+18,
自變量的取值范圍為-8<x<0;
(3)當點P在直線EF上運動到時:y=![]() x+6,
x+6,
設P點坐標是:(x,![]() x+6),
x+6),
S△OPA =![]() ×|OA|×|
×|OA|×|![]() x+6|=
x+6|=![]() ×6×|
×6×|![]() x+6|=|
x+6|=|![]() x+18|=15,
x+18|=15,
解得x=![]() 或
或![]() ,
,
當x=![]() 時,y=
時,y=![]() ×(
×(![]() )+6=5,
)+6=5,
當x=![]() 時,y=
時,y=![]() ×(
×(![]() )+6=-5
)+6=-5
即當P點的坐標是(![]() ,5)或(
,5)或(![]() ,-5)時,△OQA的面積為15.
,-5)時,△OQA的面積為15.


科目:初中數學 來源: 題型:
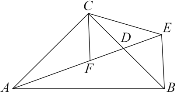
【題目】如圖,在△ABC中,∠ACB = 90°,AC = BC,D為BC邊的中點,BE⊥AB交AD的延長線于點E,CF平分∠ACB交AD于點F,連接CE.求證:(1)點D是EF的中點;(2)△CEF是等腰三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示:某一蓄水池的排水速度![]() 與排水時間
與排水時間![]() 之間的函數關系圖象
之間的函數關系圖象
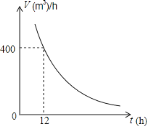
![]() 根據圖象求該蓄水池的蓄水量.
根據圖象求該蓄水池的蓄水量.
![]() 若要用不超過
若要用不超過![]() 小時的時間排完蓄水池內的水,那么每小時至少應排水多少
小時的時間排完蓄水池內的水,那么每小時至少應排水多少![]() ?
?
![]() 如果每小時排水
如果每小時排水![]() ,則排完蓄水池中的水需要多長時間?
,則排完蓄水池中的水需要多長時間?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,E是AD邊的中點,BE⊥AC于點F,連接DF,分析下列五個結論:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四邊形CDEF=![]() S△ABF,其中正確的結論有________個。
S△ABF,其中正確的結論有________個。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,CA⊥BC,垂足為C,AC=2Cm,BC=6cm,射線BM⊥BQ,垂足為B,動點P從C點出發以1cm/s的速度沿射線CQ運動,點N為射線BM上一動點,滿足PN=AB,隨著P點運動而運動,當點P運動_______秒時,△BCA與點P、N、B為頂點的三角形全等.(2個全等三角形不重合)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道,在平面內,如果一個圖形繞著一個定點旋轉一定的角度后能與自身重合,那么就稱這個圖形是旋轉對稱圖形,轉的這個角稱為這個圖形的一個旋轉角.例如,正方形繞著它的對角線的交點旋轉![]() 后能與自身重合所以正方形是旋轉對稱圖形,它有一個旋轉角為
后能與自身重合所以正方形是旋轉對稱圖形,它有一個旋轉角為![]() .
.

![]() 判斷下列說法是否正確(在相應橫線里填上“對”或“錯”)
判斷下列說法是否正確(在相應橫線里填上“對”或“錯”)
①正五邊形是旋轉對稱圖形,它有一個旋轉角為![]() .________
.________
②長方形是旋轉對稱圖形,它有一個旋轉角為![]() .________
.________
![]() 填空:下列圖形中時旋轉對稱圖形,且有一個旋轉角為
填空:下列圖形中時旋轉對稱圖形,且有一個旋轉角為![]() 的是________.(寫出所有正確結論的序號)
的是________.(寫出所有正確結論的序號)
①正三角形②正方形③正六邊形④正八邊形
![]() 寫出兩個多邊形,它們都是旋轉對稱圖形,都有一個旋轉角為
寫出兩個多邊形,它們都是旋轉對稱圖形,都有一個旋轉角為![]() ,其中一個是軸對稱圖形,但不是中心對稱圖形;另一個既是軸對稱圖形,又是中心對稱圖形.
,其中一個是軸對稱圖形,但不是中心對稱圖形;另一個既是軸對稱圖形,又是中心對稱圖形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com