
 的中點,連接PA,PB,PC.
的中點,連接PA,PB,PC. 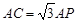 ;
;
 ,求
,求 的值.
的值.

 .設FC=24a,根據勾股定理可得OC=OA=25a,則OF=7a,AF=32a.在Rt△AFC中,根據勾股定理可表示出AC的長,在Rt△AGE和Rt△AFC中,根據三角函數的定義求解即可.
.設FC=24a,根據勾股定理可得OC=OA=25a,則OF=7a,AF=32a.在Rt△AFC中,根據勾股定理可表示出AC的長,在Rt△AGE和Rt△AFC中,根據三角函數的定義求解即可.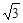 AP;
AP;
 .
. ,
, ,
, .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源:不詳 題型:解答題

 ,求OD的長度.
,求OD的長度.查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題

| A.扇形甲的圓心角是72° | B.學生的總人數是900人 |
| C.丙校的人數比乙校的人數多180人 | D.甲校的人數比丙校的人數少180人 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com