
【題目】圖書管理員小張要騎車從學校到教育局,一出校門,遇到了王老師,王老師說:“今天有風,而且去時逆風,要吃虧了”,小張回答說:“去時逆風,回來時順風,和無風往返一趟所用時間相同”.(順風速度=無風時騎車速度+風速,逆風速度=無風時騎車速度-風速)
(1)如果學校到教育局的路程是15 km,無風時小張騎自行車的速度是20 km/h,他逆風去教育局所用時間是順風回學校所用時間的![]() 倍,求風速是多少?
倍,求風速是多少?
(2)如果設從學校到教育局的路程為s千米,無風時騎車速度為v千米/時,風速為a千米/時(v>a),那么有風往返一趟的時間 無風往返一趟的時間(填“>”、“<”或“=”),試說明理由.
【答案】(1)當天的風速為5 km/h;(2)>,理由詳見解析.
【解析】
(1)首先設當天的風速為x km/h,則順風的速度為(20+x)千米/時,逆風速度是(20-x)千米/時,根據(jù)逆風去教育局所用時間是順風回學校所用時間的![]() 倍列出方程即可;
倍列出方程即可;
(2)無風時的時間=總路程÷無風時的速度;有風時的時間=單程的路程÷順風的速度+單程的路程÷逆風的速度,進而讓兩個代數(shù)式相減,根據(jù)作差比較法可知結(jié)論.
解:(1)設當天的風速為x km/h.根據(jù)題意,得
![]() =
=![]() .
.
解這個方程,得x=5.
經(jīng)檢驗,x=5是所列方程的解.
答:當天的風速為5 km/h.
(2)>,理由如下:
有風往返一趟的時間為(![]() )小時,無風往返一趟的時間為
)小時,無風往返一趟的時間為![]() 小時.
小時.
∵![]() -
-![]() =
=![]() ,
,
又∵v>a,
∴![]() >0,即
>0,即![]() >
>![]() .
.
∴有風往返一趟的時間>無風往返一趟的時間.


科目:初中數(shù)學 來源: 題型:
【題目】如圖,四邊形ABCD為平行四邊形,∠BAD的角平分線AF交CD于點E,交BC的延長線于點F. 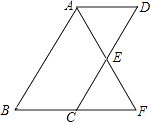
(1)求證:BF=CD;
(2)連接BE,若BE⊥AF,∠BFA=60°,BE=2 ![]() ,求平行四邊形ABCD的周長.
,求平行四邊形ABCD的周長. 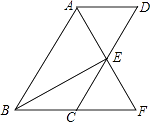
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,C、D兩點將線段AB分為三部分,AC:CD:DB=2:3:4,且AC=4.M是線段AB的中點,N是線段DB的中點.
(1)求線段DB、AB的長.
(2)求線段MN的長.
![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
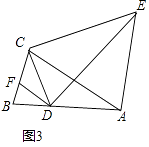
【題目】已知△ABC中,D為AB邊上任意一點,DF∥AC交BC于F,AE∥BC,∠CDE=∠ABC=∠ACB=α.
(1)如圖1,當α=60°時,求證:△DCE是等邊三角形;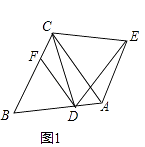
(2)如圖2,當α=45°時,求證:① ![]() =
= ![]() ;②CE⊥DE.
;②CE⊥DE.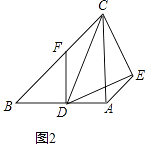
(3)如圖3,當α為任意銳角時,請直接寫出線段CE與DE的數(shù)量關(guān)系是: ![]() = .
= . 
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,已知AB∥CD,C在D的右側(cè),BE平分∠ABC,DE平分∠ADC,BE、DE所在直線交于點E,∠ADC=70°.
(1)求∠EDC的度數(shù);
(2)若∠ABC=n°,求∠BED的度數(shù)(用含n的代數(shù)式表示);
(3)將線段BC沿DC方向平移,使得點B在點A的右側(cè),其他條件不變,畫出圖形并判斷∠BED的度數(shù)是否改變,若改變,求出它的度數(shù)(用含n的式子表示);若不改變,請說明理由.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在平面直角坐標系xOy中,拋物線y=x2﹣(k+1)x+k與x軸相交于A、B兩點(點B位于點A的左側(cè)),與y軸相交于點C.
(1)如圖1,若k=2,直接寫出AB的長:AB= . 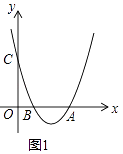
(2)若AB=2,則k的值為 .
(3)如圖2,若k=﹣3,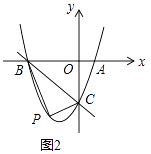
①求直線BC的解析式;
(4)如圖3,若k<0,且△ABC是等腰三角形,求k的值.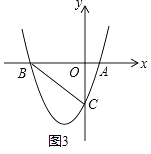
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】重慶某中學組織七、八、九年級學生參加“直轄20年,點贊新重慶”作文比賽,該校將收到的參賽作文進行分年級統(tǒng)計,繪制了如圖1和如圖2兩幅不完整的統(tǒng)計圖,根據(jù)圖中提供的信息完成以下問題. 
(1)扇形統(tǒng)計圖中九年級參賽作文篇數(shù)對應的圓心角是度,并補全條形統(tǒng)計圖;
(2)經(jīng)過評審,全校有4篇作文榮獲特等獎,其中有一篇來自七年級,學校準備從特等獎作文中任選兩篇刊登在校刊上,請利用畫樹狀圖或列表的方法求出七年級特等獎作文被選登在校刊上的概率.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
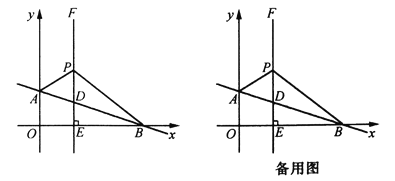
【題目】如圖,在平面直角坐標系中,直線AB:![]() 交
交![]() 軸于點
軸于點![]() ,交
,交![]() 軸于點
軸于點![]() .過點
.過點![]() 作
作![]() 軸的垂線
軸的垂線![]() 交
交![]() 于點
于點![]() ,點
,點![]() 從點
從點![]() 出發(fā),沿著射線
出發(fā),沿著射線![]() 的方向向上運動,設
的方向向上運動,設![]() .
.
(1)直線![]() 的函數(shù)表達式;
的函數(shù)表達式;
(2)求![]() 的面積(用含
的面積(用含![]() 的代數(shù)式表示);
的代數(shù)式表示);
(3)若以![]() 為直角頂點,
為直角頂點,![]() 為直角邊在第一象限作等腰直角三角形
為直角邊在第一象限作等腰直角三角形![]() ,隨著點
,隨著點![]() 的運動,點
的運動,點![]() 是否也在同一直線上運動?若在同一直線上運動,請求出直線表達式;若不在同一直線上運動,請說明理由.
是否也在同一直線上運動?若在同一直線上運動,請求出直線表達式;若不在同一直線上運動,請說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com