
【題目】如圖,拋物線y=ax2+bx+c(a≠0)與y軸交于點C(0,4),與x軸交于點A和點B,其中點A的坐標為(﹣2,0),拋物線的對稱軸x=1與拋物線交于點D,與直線BC交于點E. 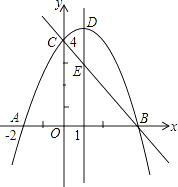
(1)求拋物線的解析式;
(2)若點F是直線BC上方的拋物線上的一個動點,是否存在點F使四邊形ABFC的面積為17,若存在,求出點F的坐標;若不存在,請說明理由;
(3)平行于DE的一條動直線l與直線BC相交于點P,與拋物線相交于點Q,若以D、E、P、Q為頂點的四邊形是平行四邊形,求點P的坐標.
【答案】
(1)解:∵拋物線y=ax2+bx+c(a≠0)過點C(0,4),
∴c=4 ①.
∵對稱軸x=﹣ ![]() =1,
=1,
∴b=﹣2a ②.
∵拋物線過點A(﹣2,0),
∴0=4a﹣2b+c ③,
由①②③解得,a=﹣ ![]() ,b=1,c=4,
,b=1,c=4,
∴拋物線的解析式為y=﹣ ![]() x2+x+4
x2+x+4
(2)解:方法一:假設存在滿足條件的點F,如圖所示,連結BF、CF、OF,過點F作FH⊥x軸于點H,FG⊥y軸于點G.
設點F的坐標為(t,﹣ ![]() t2+t+4),其中0<t<4,
t2+t+4),其中0<t<4,
則FH=﹣ ![]() t2+t+4,FG=t,
t2+t+4,FG=t,
∴S△OBF= ![]() OBFH=
OBFH= ![]() ×4×(﹣
×4×(﹣ ![]() t2+t+4)=﹣t2+2t+8,
t2+t+4)=﹣t2+2t+8,
S△OFC= ![]() OCFG=
OCFG= ![]() ×4×t=2t,
×4×t=2t,
∴S四邊形ABFC=S△AOC+S△OBF+S△OFC=4﹣t2+2t+8+2t=﹣t2+4t+12.
令﹣t2+4t+12=17,
即t2﹣4t+5=0,
則△=(﹣4)2﹣4×5=﹣4<0,
∴方程t2﹣4t+5=0無解,
故不存在滿足條件的點F
方法二:
∵B(4,0),C(0,4),
∴lBC:y=﹣x+4,
過F點作x軸垂線,交BC于H,設F(t,﹣ ![]() t2+t+4),
t2+t+4),
∴H(t,﹣t+4),
∵S四邊形ABFC=S△ABC+S△BCF=17,
∴ ![]() (4+2)×4+
(4+2)×4+ ![]() (﹣
(﹣ ![]() t2+t+4+t﹣4)×4=17,
t2+t+4+t﹣4)×4=17,
∴t2﹣4t+5=0,
∴△=(﹣4)2﹣4×5<0,
∴方程t2﹣4t+5=0無解,故不存在滿足條件的點F
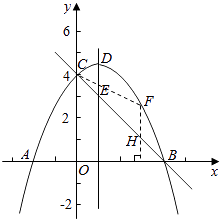
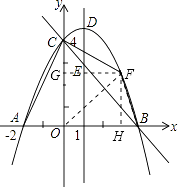
(3)解:方法一:設直線BC的解析式為y=kx+n(k≠0),
∵B(4,0),C(0,4),
∴ ![]() ,
,
解得 ![]() ,
,
∴直線BC的解析式為y=﹣x+4.
由y=﹣ ![]() x2+x+4=﹣
x2+x+4=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ,
,
∴頂點D(1, ![]() ),
),
又點E在直線BC上,則點E(1,3),
于是DE= ![]() ﹣3=
﹣3= ![]() .
.
若以D、E、P、Q為頂點的四邊形是平行四邊形,因為DE∥PQ,只須DE=PQ,
設點P的坐標是(m,﹣m+4),則點Q的坐標是(m,﹣ ![]() m2+m+4).
m2+m+4).
① 當0<m<4時,PQ=(﹣ ![]() m2+m+4)﹣(﹣m+4)=﹣
m2+m+4)﹣(﹣m+4)=﹣ ![]() m2+2m,
m2+2m,
由﹣ ![]() m2+2m=
m2+2m= ![]() ,
,
解得:m=1或3.
當m=1時,線段PQ與DE重合,m=1舍去,
∴m=3,P1(3,1).
②當m<0或m>4時,PQ=(﹣m+4)﹣(﹣ ![]() m2+m+4)=
m2+m+4)= ![]() m2﹣2m,
m2﹣2m,
由 ![]() m2﹣2m=
m2﹣2m= ![]() ,
,
解得m=2± ![]() ,經檢驗適合題意,
,經檢驗適合題意,
此時P2(2+ ![]() ,2﹣
,2﹣ ![]() ),P3(2﹣
),P3(2﹣ ![]() ,2+
,2+ ![]() ).
).
綜上所述,滿足題意的點P有三個,分別是P1(3,1),P2(2+ ![]() ,2﹣
,2﹣ ![]() ),P3(2﹣
),P3(2﹣ ![]() ,2+
,2+ ![]() )
)
方法二:
∵DE∥PQ,
∴當DE=PQ時,以D、E、P、Q為頂點的四邊形是平行四邊形,
∵y=﹣ ![]() x2+x+4,
x2+x+4,
∴D(1, ![]() ),
),
∵lBC:y=﹣x+4,
∴E(1,3),
∴DE= ![]() ﹣3=
﹣3= ![]() ,
,
設點F的坐標是(m,﹣m+4),則點Q的坐標是(m,﹣ ![]() m2+m+4),
m2+m+4),
∴|﹣m+4+ ![]() m2﹣m﹣4|=
m2﹣m﹣4|= ![]() ,
,
∴ ![]() m2﹣2m=
m2﹣2m= ![]() 或
或 ![]() m2﹣2m=﹣
m2﹣2m=﹣ ![]() ,
,
∴m=1,m=3,m=2+ ![]() ,m=2﹣
,m=2﹣ ![]() ,
,
經檢驗,當m=1時,線段PQ與DE重合,故舍去.
∴P1(3,1),P2(2+ ![]() ,2﹣
,2﹣ ![]() ),P3(2﹣
),P3(2﹣ ![]() ,2+
,2+ ![]() ).
).
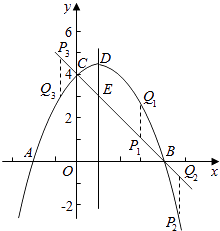
【解析】方法一:(1)先把C(0,4)代入y=ax2+bx+c,得出c=4①,再由拋物線的對稱軸x=﹣ ![]() =1,得到b=﹣2a②,拋物線過點A(﹣2,0),得到0=4a﹣2b+c③,然后由①②③可解得,a=﹣
=1,得到b=﹣2a②,拋物線過點A(﹣2,0),得到0=4a﹣2b+c③,然后由①②③可解得,a=﹣ ![]() ,b=1,c=4,即可求出拋物線的解析式為y=﹣
,b=1,c=4,即可求出拋物線的解析式為y=﹣ ![]() x2+x+4;(2)假設存在滿足條件的點F,連結BF、CF、OF,過點F作FH⊥x軸于點H,FG⊥y軸于點G.設點F的坐標為(t,﹣
x2+x+4;(2)假設存在滿足條件的點F,連結BF、CF、OF,過點F作FH⊥x軸于點H,FG⊥y軸于點G.設點F的坐標為(t,﹣ ![]() t2+t+4),則FH=﹣
t2+t+4),則FH=﹣ ![]() t2+t+4,FG=t,先根據三角形的面積公式求出S△OBF=
t2+t+4,FG=t,先根據三角形的面積公式求出S△OBF= ![]() OBFH=﹣t2+2t+8,S△OFC=
OBFH=﹣t2+2t+8,S△OFC= ![]() OCFG=2t,再由S四邊形ABFC=S△AOC+S△OBF+S△OFC , 得到S四邊形ABFC=﹣t2+4t+12.令﹣t2+4t+12=17,即t2﹣4t+5=0,由△=(﹣4)2﹣4×5=﹣4<0,得出方程t2﹣4t+5=0無解,即不存在滿足條件的點F;(3)先運用待定系數法求出直線BC的解析式為y=﹣x+4,再求出拋物線y=﹣
OCFG=2t,再由S四邊形ABFC=S△AOC+S△OBF+S△OFC , 得到S四邊形ABFC=﹣t2+4t+12.令﹣t2+4t+12=17,即t2﹣4t+5=0,由△=(﹣4)2﹣4×5=﹣4<0,得出方程t2﹣4t+5=0無解,即不存在滿足條件的點F;(3)先運用待定系數法求出直線BC的解析式為y=﹣x+4,再求出拋物線y=﹣ ![]() x2+x+4的頂點D(1,
x2+x+4的頂點D(1, ![]() ),由點E在直線BC上,得到點E(1,3),于是DE=
),由點E在直線BC上,得到點E(1,3),于是DE= ![]() ﹣3=
﹣3= ![]() .若以D、E、P、Q為頂點的四邊形是平行四邊形,因為DE∥PQ,只須DE=PQ,設點P的坐標是(m,﹣m+4),則點Q的坐標是(m,﹣
.若以D、E、P、Q為頂點的四邊形是平行四邊形,因為DE∥PQ,只須DE=PQ,設點P的坐標是(m,﹣m+4),則點Q的坐標是(m,﹣ ![]() m2+m+4).分兩種情況進行討論:①當0<m<4時,PQ=(﹣
m2+m+4).分兩種情況進行討論:①當0<m<4時,PQ=(﹣ ![]() m2+m+4)﹣(﹣m+4)=﹣
m2+m+4)﹣(﹣m+4)=﹣ ![]() m2+2m,解方程﹣
m2+2m,解方程﹣ ![]() m2+2m=
m2+2m= ![]() ,求出m的值,得到P1(3,1);②當m<0或m>4時,PQ=(﹣m+4)﹣(﹣
,求出m的值,得到P1(3,1);②當m<0或m>4時,PQ=(﹣m+4)﹣(﹣ ![]() m2+m+4)=
m2+m+4)= ![]() m2﹣2m,解方程
m2﹣2m,解方程 ![]() m2﹣2m=
m2﹣2m= ![]() ,求出m的值,得到P2(2+
,求出m的值,得到P2(2+ ![]() ,2﹣
,2﹣ ![]() ),P3(2﹣
),P3(2﹣ ![]() ,2+
,2+ ![]() ).方法二:(1)略.(2)利用水平底與鉛垂高乘積的一半,可求出△BCF的面積函數,進而求出點F坐標,因為,所以無解.(3)因為PQ∥DE,所以只需PQ=AC即可,求出PQ的參數長度便可列式求解.
).方法二:(1)略.(2)利用水平底與鉛垂高乘積的一半,可求出△BCF的面積函數,進而求出點F坐標,因為,所以無解.(3)因為PQ∥DE,所以只需PQ=AC即可,求出PQ的參數長度便可列式求解.
【考點精析】認真審題,首先需要了解確定一次函數的表達式(確定一個一次函數,需要確定一次函數定義式y=kx+b(k不等于0)中的常數k和b.解這類問題的一般方法是待定系數法),還要掌握平行四邊形的判定(兩組對邊分別平行的四邊形是平行四邊形:兩組對邊分別相等的四邊形是平行四邊形;一組對邊平行且相等的四邊形是平行四邊形;兩組對角分別相等的四邊形是平行四邊形;對角線互相平分的四邊形是平行四邊形)的相關知識才是答題的關鍵.


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:初中數學 來源: 題型:
【題目】如圖,在⊙O中,AB是直徑,點D是⊙O上一點,點C是弧AD的中點,弦CE⊥AB于點E,過點D的切線交EC的延長線于點G,連接AD,分別交CE、CB于點P、Q,連接AC,給出下列結論:①∠DAC=∠ABC;②AD=CB;③點P是△ACQ的外心;④AC2=AEAB;⑤CB∥GD,其中正確的結論是( ) 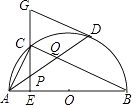
A.①③⑤
B.②④⑤
C.①②⑤
D.①③④
查看答案和解析>>
科目:初中數學 來源: 題型:
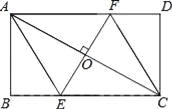
【題目】如圖,AC是矩形ABCD的對角線,過AC的中點O作EF⊥AC,交BC于點E,交AD于點F,連接AE,CF.
(1)求證:四邊形AECF是菱形;
(2)若AB=![]() ,∠DCF=30°,求四邊形AECF的面積.(結果保留根號)
,∠DCF=30°,求四邊形AECF的面積.(結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,E是AB上一點,BE=2,AE=3,P是AC上一動點,則PB+PE的最小值是( ).

A. 5 B. 5![]() C. 6 D.
C. 6 D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
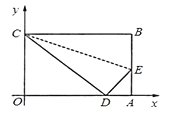
【題目】如圖,四邊形OABC是一張放在平面直角坐標系中的矩形紙片,點A在x軸上,點C在y軸上,A點坐標為(10, 0),C點坐標為(0, 6),將邊BC折疊,使點B落在邊OA上的點D處,求線段EA 的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1的正方形組成的網格中,△AOB的頂點均在格點上,點A、B的坐標分別是A(3,2),B(1,3),△AOB繞點O逆時針旋轉90°后得到△A1OB1 . 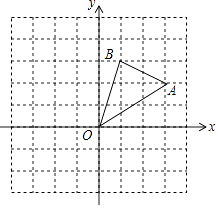
(1)點A關于點O中心對稱的點P的坐標為;
(2)在網格內畫出△A1OB1;
(3)點A1、B1的坐標分別為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,對角線AC、BD交于點O.M為AD中點,連接CM交BD于點N,且ON=1. 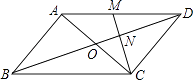
(1)求BD的長;
(2)若△DCN的面積為2,求四邊形ABNM的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先化簡,再求值,
(1)2x2y﹣[3xy2+2(xy2+2x2y)],其中x=![]() ,y=﹣2.
,y=﹣2.
(2)已知a+b=4,ab=﹣2,求代數式(4a﹣3b﹣2ab)﹣(a﹣6b﹣ab)的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com