
【題目】如圖,CN是等邊△![]() 的外角
的外角![]() 內(nèi)部的一條射線,點A關(guān)于CN的對稱點為D,連接AD,BD,CD,其中AD,BD分別交射線CN于點E,P.
內(nèi)部的一條射線,點A關(guān)于CN的對稱點為D,連接AD,BD,CD,其中AD,BD分別交射線CN于點E,P.
(1)依題意補全圖形;
(2)若![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示);
的式子表示);
(3)用等式表示線段![]() ,
, ![]() 與
與![]() 之間的數(shù)量關(guān)系,并證明.
之間的數(shù)量關(guān)系,并證明.

【答案】(1)圖形見解析(2)∠BDC=60°-α(3)PB=PC+2PE
【解析】試題分析:(1)按題意補全圖形即可;
(2)由點A與點D關(guān)于CN對稱可得CA=CD,再由∠ACN=α得到∠ACD=2α,由等邊△ABC可推得∠BCD=∠ACB+∠ACD=60°+2α,從而可得;
(3)PB=PC+2PE. 在PB上截取PF使PF=PC,連接CF,通過推導(dǎo)可證明△BFC≌△DPC,再利用全等三角形的對應(yīng)邊相等即可得.
試題解析:(1)如圖所示;
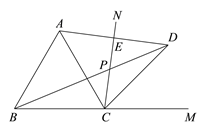
(2)∵點A與點D關(guān)于CN對稱,
∴CN是AD的垂直平分線,
∴CA=CD,
∵![]() ,
,
∴∠ACD=2![]() ,
,
∵等邊△ABC,
∴CA=CB=CD,∠ACB=60°,
∴∠BCD=∠ACB+∠ACD=60°+![]() ,
,
∴∠BDC=∠DBC=![]() (180°
(180°![]() ∠BCD)=60°
∠BCD)=60°![]()
![]() ;
;
(3)結(jié)論:PB=PC+2PE.
本題證法不唯一,如:
在PB上截取PF使PF=PC,連接CF.
∵CA=CD,∠ACD=![]()
∴∠CDA=∠CAD=90°![]()
![]() .
.
∵∠BDC=60°![]()
![]() ,
,
∴∠PDE=∠CDA![]() ∠BDC=30°
∠BDC=30°
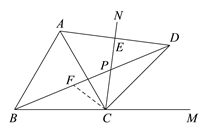
∴PD=2PE.
∵∠CPF=∠DPE=90°![]() ∠PDE=60°.
∠PDE=60°.
∴△CPF是等邊三角形.
∴∠CPF=∠CFP=60°.
∴∠BFC=∠DPC=120°.
∴在△BFC和△DPC中,
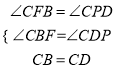 ,
,
∴△BFC≌△DPC.
∴BF=PD=2PE.
∴PB= PF+BF=PC+2PE.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】推理填空:如圖,E點為DF上的點,B為AC上的點, ![]() ,那么
,那么![]() ,請完成它成立的理由
,請完成它成立的理由
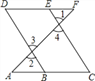
解: ![]() ______
______ ![]()
又![]()
![]() ______
______ ![]()
![]() ______
______ ![]() ______
______ ![]() ______
______ ![]()
![]() ______
______ ![]()
![]() ______
______ ![]()
![]() ______
______ ![]()
![]() ______
______ ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某公司投資某個工程項目,現(xiàn)在甲、乙兩個工程隊有能力承包這個項目.公司調(diào)查發(fā)現(xiàn):乙隊單獨完成工程的時間是甲隊的![]() 倍;甲、乙兩隊合作完成工程需要
倍;甲、乙兩隊合作完成工程需要![]() 天;甲隊每天的工作費用為
天;甲隊每天的工作費用為![]() 元、乙隊每天的工作費用為
元、乙隊每天的工作費用為![]() 元.根據(jù)以上信息,從節(jié)約資金的角度考慮,公司應(yīng)選擇哪個工程隊、應(yīng)付工程隊費用多少元?
元.根據(jù)以上信息,從節(jié)約資金的角度考慮,公司應(yīng)選擇哪個工程隊、應(yīng)付工程隊費用多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,∠B=∠C=90°,M是BC的中點,DM平分∠ADC,則AM平分∠DAB嗎?試說明理由。(提示:過點M作ME垂直AD于E)。

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,AB是⊙O的直徑,C是⊙O上一點,OD⊥BC于點D,過點C作⊙O的切線,交OD的延長線于點E,連接BE.
(1)求證:BE與⊙O相切;
(2)設(shè)OE交⊙O于點F,若DF=1,BC=2![]() ,求陰影部分的面積.
,求陰影部分的面積.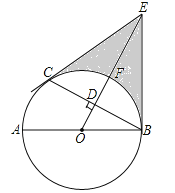
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系xOy中,點P(1,0).點P第1次向上跳動1個單位至點P1(1,1),緊接著第2次向左跳動2個單位至點P2(-1,1),第3次向上跳動1個單位至點P3,第4次向右跳動3個單位至點P4,第5次又向上跳動1個單位至點P5,第6次向左跳動4個單位至點P6,…….照此規(guī)律,點P第100次跳動至點P100的坐標(biāo)是( )

A. (-26,50) B. (-25,50) C. (26,50) D. (25,50)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
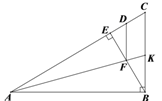
【題目】如圖,在△ABC中,∠ABC=90°,BE⊥AC于點E,點D在AC上,且AD=AB,AK平分∠CAB,交線段BE于點F,交邊CB于點K.
(1)在圖中找出一對全等三角形,并證明;
(2)求證:FD∥BC .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】對于0,1以及真分數(shù)p,q,r,若p<q<r,我們稱q為p和r的中間分數(shù).為了幫助我們找中間分數(shù),制作了下表:
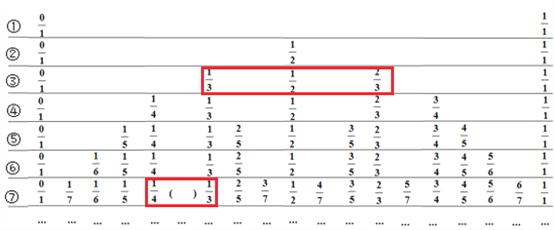
兩個不等的正分數(shù)有無數(shù)多個中間分數(shù).例如:上表中第③行中的3個分數(shù)![]() 、
、![]() 、
、![]() ,有
,有![]() ,所以
,所以![]() 為
為![]() 和
和![]() 的一個中間分數(shù),在表中還可以找到
的一個中間分數(shù),在表中還可以找到![]() 和
和![]() 的中間分數(shù)
的中間分數(shù)![]() ,
, ![]() ,
, ![]() ,
, ![]() .把這個表一直寫下去,可以找到
.把這個表一直寫下去,可以找到![]() 和
和![]() 更多的中間分數(shù).
更多的中間分數(shù).
(1)按上表的排列規(guī)律,完成下面的填空:
①上表中括號內(nèi)應(yīng)填的數(shù)為 ;
②如果把上面的表一直寫下去,那么表中第一個出現(xiàn)的![]() 和
和![]() 的中間分數(shù)是 ;
的中間分數(shù)是 ;
(2)寫出分數(shù)![]() 和
和![]() (a、b、c、d均為正整數(shù),
(a、b、c、d均為正整數(shù), ![]() ,
, ![]() )的一個中間分數(shù)(用含a、b、c、d的式子表示),并證明;
)的一個中間分數(shù)(用含a、b、c、d的式子表示),并證明;
(3)若![]() 與
與![]() (m、n、s、 t均為正整數(shù))都是
(m、n、s、 t均為正整數(shù))都是![]() 和
和![]() 的中間分數(shù),則
的中間分數(shù),則![]() 的最小值為 .
的最小值為 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
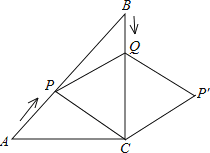
【題目】如圖,在Rt△ABC中,∠C=90°,AC=BC=6cm,點P從點A出發(fā),沿AB方向以每秒![]() cm的速度向終點B運動;同時,動點Q從點B出發(fā)沿BC方向以每秒1cm的速度向終點C運動,將△PQC沿BC翻折,點P的對應(yīng)點為點P′.設(shè)點Q運動的時間為t秒,若四邊形QPCP′為菱形,則t的值為( )
cm的速度向終點B運動;同時,動點Q從點B出發(fā)沿BC方向以每秒1cm的速度向終點C運動,將△PQC沿BC翻折,點P的對應(yīng)點為點P′.設(shè)點Q運動的時間為t秒,若四邊形QPCP′為菱形,則t的值為( )
A.![]() B.2 C.2
B.2 C.2![]() D.3
D.3
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com