【題目】已知二次函數
的圖象如圖所示，對稱軸為
．下列結論中，正確的是（ ）
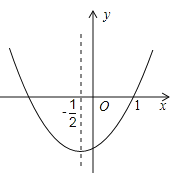
A.
B.
C.
D.
【答案】D
【解析】
由二次函數的性質，即可確定a，b，c的符號，即可判定A是錯誤的；又由對稱軸為
，即可求得a=b，可判定B錯誤；由b＞0，c＜0，即可判定C錯誤；然后由拋物線與x軸交點坐標的特點，判定D正確．
∵開口向上，
∴a＞0，
∵拋物線與y軸交于負半軸，
∴c＜0，
∵對稱軸在y軸左側，
∴
，
∴b＞0，
∴abc＜0，
故A選項錯誤；
B、∵對稱軸：
，
∴a=b，
∴
，故B選項錯誤；
C、∵b＞0，c＜0，
∴
，
故C選項錯誤；
D、∵對稱軸為，與x軸的一個交點的取值范圍為x1＞1，
∴與x軸的另一個交點的取值范圍為x2＜-2，
∴當x=-2時，4a-2b+c＜0，
即4a+c＜2b，
故D選項正確；
故答案為：D．
新思維假期作業暑假吉林大學出版社系列答案
藍天教育暑假優化學習系列答案科目：初中數學 來源： 題型：
【題目】如圖是某班甲、乙、丙三位同學最近5次數學成績及其所在班級相應平均分的折線統計圖，則下列判斷錯誤的是( ).
A. 甲的數學成績高于班級平均分，且成績比較穩定
B. 乙的數學成績在班級平均分附近波動，且比丙好
C. 丙的數學成績低于班級平均分，但成績逐次提高
D. 就甲、乙、丙三個人而言，乙的數學成績最不穩
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了幫助遭受自然災害的地區，某學校號召同學們自愿捐款，已知第一次捐款總額為5800元，第二次捐款總額6000元，第二次捐款人數比第一次多20人，而且兩次人均捐款額正好相等．
|
| |
每桶容積（升） | 20 | 15 |
每桶價格（元） | 5.6 | 4.5 |
（1）求兩次各有多少人捐款？
（2）民政部門要求將捐款換成實物，統一運送到災區．學校決定將捐款用于購買桶裝水現有
兩種型號桶裝水，上表是這兩種桶裝水的容積和單價．學校按民政局的救災規劃需訂購總容積為40000升的桶裝水，用同學們的捐款至少需訂購
型水多少桶．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】博文書店舉行購書優惠活動：
①一次性購書不超過100元，不享受打折優惠；
②一次性購書超過100元但不超過200元一律打九折；
③一次性購書200元以上一律打七折．
小麗在這次活動中，兩次購書總共付款229.4元，第二次購書原價是第一次購書原價的3倍，那么小麗這兩次購書原價的總和是多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某種型號油電混合動力汽車，從A地到B地燃油行駛純燃油費用76元，從A地到B地用電行駛純電費用26元，已知每行駛1千米，純燃油費用比純用電費用多0.5元．
（1）求每行駛1千米純用電的費用；
（2）若要使從A地到B地油電混合行駛所需的油、電費用合計不超過39元，則至少用電行駛多少千米？
查看答案和解析>>
科目：初中數學 來源： 題型：
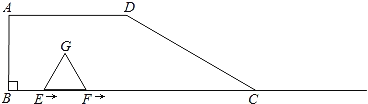
【題目】如圖，四邊形ABCD中，AD∥BC，∠B＝90°，BC＝6，AD＝3，∠DCB＝30°，點E、F同時從B點出發，沿射線BC向右勻速移動．已知F點移動速度是E點移動速度的2倍，以EF為一邊在CB的上方作等邊△EFG．設E點移動距離為x（0＜x＜6）．
（1）點G在四邊形ABCD的邊上時，x＝ ；點F與點C重合時，x＝ ；
（2）求出使△DFC成為等腰三角形的x的值；
（3）求△EFG與四邊形ABCD重疊部分的面積y與x之間的函數關系式，并直接寫出y的最大值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線
與
軸交于點
，與
軸交于點
，且與雙曲線
的一個交點為
，將直線
在軸下方的部分沿軸翻折，得到一個“
”形折線
的新函數．若點
是線段
上一動點（不包括端點），過點作軸的平行線，與新函數交于另一點
，與雙曲線交于點
．
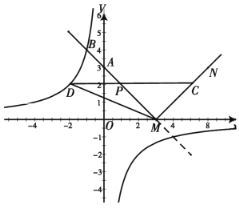
（1）若點的橫坐標為
，求
的面積；（用含的式子表示）
（2）探索：在點的運動過程中，四邊形
能否為平行四邊形？若能，求出此時點的坐標；若不能，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一次函數
的圖像與反比例函數
的圖像交于
，
兩點，與
軸分別交于
兩點，且
．
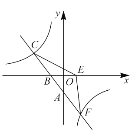
（1）求一次函數和反比例函數的解析式；
（2）若點
與點
關于
軸對稱，連接
，求
的面積．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
