
【題目】已知函數![]() 與x軸、y軸分別交于A、B兩點,C點坐標是(0,2),連接AC.
與x軸、y軸分別交于A、B兩點,C點坐標是(0,2),連接AC.

(1)直接寫出A、B兩點的坐標:A(______,_____)、B(_____,_____);
(2)在AB上找一點P,當PC+PO最小時,在AC上找一點Q使得PQ+![]() 最小,求Q點坐標;
最小,求Q點坐標;
(3)在(2)的條件下,平面內能否找到一點K,使得點A、C、P、K構成的四邊形是平行四邊形,若能,直接寫出K點坐標,若不能,請說明理由.
【答案】(1)(![]() ,0),(0,6);(2)Q(
,0),(0,6);(2)Q(![]() );(3)能,K(
);(3)能,K(![]() ,
,![]() )或K(
)或K(![]() ,
,![]() )或K(
)或K(![]() ,
,![]() ).
).
【解析】
(1)在一次函數解析式中,分別令y=0和x=0即可求出A、B的坐標;
(2)作點O關于AB的對稱點O′,連接C O′與AB交于P點,則P點即為使得CP+OP最小的點.過O′作O′D⊥x軸.可求出 O′的坐標,O′C的解析式.由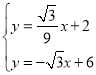 得P的坐標.過Q作QH⊥x軸于H,與AC交于Q點.由含30°直角三角形的性質可得QH=
得P的坐標.過Q作QH⊥x軸于H,與AC交于Q點.由含30°直角三角形的性質可得QH=![]() AQ,即可得到當PH⊥x軸時與AC交點Q即為所求,即可得出點Q的坐標;
AQ,即可得到當PH⊥x軸時與AC交點Q即為所求,即可得出點Q的坐標;
(3)設K(x,y),點A、C、P、K構成的四邊形是平行四邊形,分三種情況討論:
①若AK,CP是對角線;②若AP,CK是對角線;③若AC,KP是對角線,;分別利用平行四邊形對角線的交點平分對角線和中點坐標公式即可得出點K的坐標.
(1)在![]() 中,令y=0,解得:x=
中,令y=0,解得:x=![]() ,令x=0,解得:y=6,∴A(
,令x=0,解得:y=6,∴A(![]() ,0),B(0,6);
,0),B(0,6);
(2)作點O關于AB的對稱點O′,連接C O′與AB交于P點,則P點即為使得CP+OP最小的點.過O′作O′D⊥x軸.
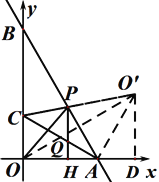
∵OA=![]() ,OB=6,∴AB=
,OB=6,∴AB=![]() ,∴∠ABO=30,∠BAO=60,∴O′A=OA=
,∴∠ABO=30,∠BAO=60,∴O′A=OA=![]() ,∠O′AB=∠OAB=60 ∴∠O'AD=60°,∴∠AO'D=30°,∴O′D=3,AD=
,∠O′AB=∠OAB=60 ∴∠O'AD=60°,∴∠AO'D=30°,∴O′D=3,AD=![]() ,∴ O′(
,∴ O′(![]() ,3),易求O′C解析式為:
,3),易求O′C解析式為:![]() .
.
由 得P(
得P(![]() ,
,![]() ).
).
過Q作QH⊥x軸于H,與AC交于Q點.
∵OC=2,OA=![]() ,∴∠CAO=30,∴QH=
,∴∠CAO=30,∴QH=![]() AQ,∴當PH⊥x軸時與AC交點Q即為所求.
AQ,∴當PH⊥x軸時與AC交點Q即為所求.
易求直線AC的解析式為![]() ,把x=
,把x=![]() 代入
代入![]() ,得y=
,得y=![]() ,∴Q(
,∴Q(![]() ).
).
(3)設K(x,y).
∵P(![]() ,
,![]() ),A(
),A(![]() ,0),C(0,2),點A、C、P、K構成的四邊形是平行四邊形,∴分三種情況討論:
,0),C(0,2),點A、C、P、K構成的四邊形是平行四邊形,∴分三種情況討論:
①若AK,CP是對角線,則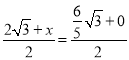 ,
,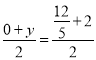 ,解得:x=
,解得:x=![]() ,y=
,y=![]() ,∴ K(
,∴ K(![]() ,
,![]() );
);
②若AP,CK是對角線,則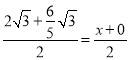 ,
,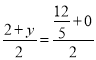 ,解得:x=
,解得:x=![]() ,y=
,y=![]() ,∴ K(
,∴ K(![]() ,
,![]() );
);
③若AC,KP是對角線,則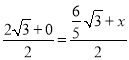 ,
,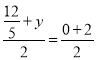 ,解得:x=
,解得:x=![]() ,y=
,y=![]() ,∴ K(
,∴ K(![]() ,
,![]() );
);
綜上所述:K(![]() ,
,![]() )或K(
)或K(![]() ,
,![]() )或K(
)或K(![]() ,
,![]() ).
).


科目:初中數學 來源: 題型:
【題目】下列說法,其中正確的個數是( )
①整數和分數統稱為有理數;②絕對值是它本身的數只有0;③兩數之和一定大于每個加數;④如果兩個數積為0,那么至少有一個因數為0;⑤0是最小的有理數,;⑥數軸上表示互為相反數的點位于原點的兩側;⑦幾個有理數相乘,如果負因數的個數是奇數,那么積為負數,
A.5個B.4個C.3個D.2個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+bx+c的圖象與x軸交于A、B兩點,與y軸交于點C,且OB=OC,下列結論:①b>1且b≠2;②b2﹣4ac<4a2;③a>![]() ;其中正確的個數為( )
;其中正確的個數為( )

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,PA、PB是⊙O的切線,A、B為切點,∠APB=60°,連接PO并延長與⊙O交于C點,連接AC,BC.
(1)求證:四邊形ACBP是菱形;

(2)若⊙O半徑為1,求菱形ACBP的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:矩形ABCD中,AB=4,BC=3,點M、N分別在邊AB、CD上,直線MN交矩形對角線 AC于點E,將△AME沿直線MN翻折,點A落在點P處,且點P在射線CB上.
(1)如圖1,當EP⊥BC時,求CN的長;
(2) 如圖2,當EP⊥AC時,求AM的長;
(3) 請寫出線段CP的長的取值范圍,及當CP的長最大時MN的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
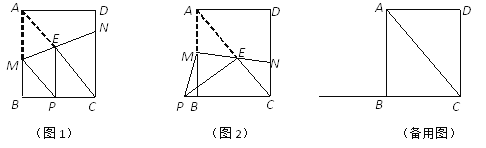
【題目】如圖,已知AM∥BN,∠A=60°.點P是射線AM上一動點(與點A不重合),BC、BD分別平分∠ABP和∠PBN,分別交射線AM于點C,D.
(1)求∠CBD的度數;
(2)當點P運動時,∠APB與∠ADB之間的數量關系是否隨之發生變化?若不變化,請寫出它們之間的關系,并說明理由;若變化,請寫出變化規律.
(3)當點P運動到使∠ACB=∠ABD時,直接寫出∠ABC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,將一個圓依次二等分、三等分、四等分、五等分…,并按圖中規律在半徑上擺放黑色棋子,則第一幅圖中有5個棋子,第二幅圖中有10個棋子,第三幅圖中有17個棋子,第四幅圖中有26個棋子,依此規律,則第6幅圖中所含棋子數目為( )

A.51 B.50 C.49 D.48
查看答案和解析>>
科目:初中數學 來源: 題型:
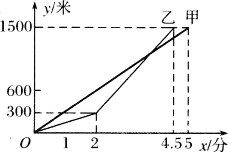
【題目】甲、乙兩人進行1500米比賽,在比賽時,兩人所跑的路程y(米)與所用的時間x(分)間的函數關系如圖所示,解答下列問題:
(1)求甲的速度等于多少米/分;
(2)當乙到終點時,甲距離終點有多遠;
(3)乙在距終點多遠處追上了甲.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在矩形ABCD中,∠ADC的平分線DE與BC邊所在的直線交于點E,點P是線段DE上一定點(其中EP<PD)
(1)如圖1,若點F在CD邊上(不與D重合),將∠DPF繞點P逆時針旋轉90°后,角的兩邊PD、PF分別交射線DA于點H、G.
①求證:PG=PF;
②探究:DF、DG、DP之間有怎樣的數量關系,并證明你的結論.
(2)拓展:如圖2,若點F在CD的延長線上(不與D重合),過點P作PG⊥PF,交射線DA于點G,你認為(1)中DE、DG、DP之間的數量關系是否仍然成立?若成立,給出證明;若不成立,請寫出它們所滿足的數量關系式,并說明理由.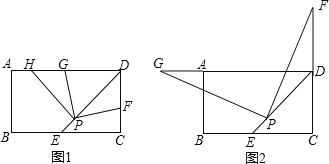
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com