
【題目】綜合與實踐
情境再現:
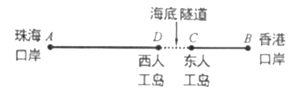
舉世矚目的港珠澳大橋東接香港,西接珠海、澳門,全長![]() 千米,是世界上最長的跨海大橋,被譽為“新世界七大奇跡”之一.如圖,香港口岸點
千米,是世界上最長的跨海大橋,被譽為“新世界七大奇跡”之一.如圖,香港口岸點![]() 至珠海口岸點
至珠海口岸點![]() 約
約![]() 千米,海底隧道
千米,海底隧道![]() 全長約
全長約![]() 千米,隧道一端的東人工島點
千米,隧道一端的東人工島點![]() 到香港口岸的路程為
到香港口岸的路程為![]() 千米.某一時刻,一輛穿梭巴士從香港口岸發車,沿港珠澳大橋開往珠海口岸.
千米.某一時刻,一輛穿梭巴士從香港口岸發車,沿港珠澳大橋開往珠海口岸.![]() 分鐘后,一輛私家車也從香港口岸出發沿港珠澳大橋開往珠海口岸.在私家車出發的同時,一輛大客車從珠海口岸出發開往香港口岸.已知穿梭巴士的平均速度為
分鐘后,一輛私家車也從香港口岸出發沿港珠澳大橋開往珠海口岸.在私家車出發的同時,一輛大客車從珠海口岸出發開往香港口岸.已知穿梭巴士的平均速度為![]() 千米/時,大客車的平均速度為
千米/時,大客車的平均速度為![]() 千米/時,私家車的平均速度為
千米/時,私家車的平均速度為![]() 千米/時.
千米/時.
問題解決:
(1)穿梭巴士出發多長時間與大客車相遇?
(2)私家車能否在到達珠海口岸前追上穿梭巴士?說明理由;
【答案】(1)穿梭巴士出發經過![]() 小時與大客車相遇;(2)私家車不能在到達珠海口岸前追上穿梭巴士,理由詳見解析.
小時與大客車相遇;(2)私家車不能在到達珠海口岸前追上穿梭巴士,理由詳見解析.
【解析】
(1)設穿梭巴士出發經過x小時與大客車相遇,根據題意,兩車的路程和為42km,即可列出方程進行求解;(2)設私家車追上穿梭巴士所用的時間為y小時,他們的路程相等,即可列出方程解得時間y,再進行比較穿梭巴士到達珠海口岸的時間,即可求解.
解:(1)設穿梭巴士出發經過![]() 小時與大客車相遇.
小時與大客車相遇.
根據題意,得![]() .
.
解這個方程,得![]() ,
,
答:穿梭巴士出發經過![]() 小時與大客車相遇.
小時與大客車相遇.
(2)私家車不能在到達珠海口岸前追上穿梭巴士,理由如下:
設私家車追上穿梭巴士所用的時間為![]() 小時,
小時,
根據題意,得![]() .
.
解這個方程,得![]() .
.
穿梭巴士到達珠海口岸的時間為![]() ,
,
因為![]() ,
,
所以私家車不能在到達珠海口岸前追上穿梭巴士.


科目:初中數學 來源: 題型:
【題目】為了更好改善河流的水質,治污公司決定購買10臺污水處理設備![]() 現有A,B兩種型號的設備,其中每臺的價格,月處理污水量如下表:經調查:購買一臺A型設備比購買一臺B型設備多2萬元,購買2臺A型設備比購買3臺B型設備少6萬元.
現有A,B兩種型號的設備,其中每臺的價格,月處理污水量如下表:經調查:購買一臺A型設備比購買一臺B型設備多2萬元,購買2臺A型設備比購買3臺B型設備少6萬元.
A型 | B型 | |
價格 | a | b |
處理污水量 | 240 | 200 |
![]() 求a,b的值;
求a,b的值;
![]() 治污公司經預算購買污水處理設備的資金不超過105萬元,你認為該公司有哪幾種購買方案;
治污公司經預算購買污水處理設備的資金不超過105萬元,你認為該公司有哪幾種購買方案;
![]() 在
在![]() 的條件下,若每月要求處理污水量不低于2040噸,為了節約資金,請你為治污公司設計一種最省錢的購買方案.
的條件下,若每月要求處理污水量不低于2040噸,為了節約資金,請你為治污公司設計一種最省錢的購買方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校組織社會大課堂活動去首都博物館參觀,明明提前上網做了功課,查到了下面的一段文字:
首都博物館建筑本身是一座融古典美和現代美于一體的建筑藝術品,既具有濃郁的民族特色,又呈現鮮明的現代感.首都博物館建筑物(地面以上)東西長152米、南北寬66米左右,建筑高度41米.建筑內部分為三棟獨立的建筑,即:矩形展館,橢圓形專題展館,條形的辦公科研樓.橢圓形的青銅展館斜出墻面寓意古代文物破土而出,散發著濃郁的歷史氣息.
明明對首都博物館建筑物產生了濃厚的興趣,站到首都博物館北廣場,他被眼前這座建筑物震撼了.整個建筑宏大壯觀,斜出的青銅展館和北墻面交出一條拋物線,拋物線與外立面之間和諧、統一,明明走到過街天橋上照了一張照片(如圖所示).明明想了想,算了算,對旁邊的文文說:“我猜想這條拋物線的頂點到地面的距離應是15.7米左右.” 文文反問:“你猜想的理由是什么”?明明說:“我的理由是”. 明明又說:“不過這只是我的猜想,這次準備不充分,下次來我要用學過的數學知識準確的測測這個高度,我想用學到的知識, 我要帶等測量工具”.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】請從下列![]() 、
、![]() 兩題中任選一題作答,我選擇: 題.
兩題中任選一題作答,我選擇: 題.
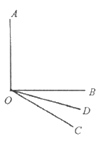
![]() :如圖,已知
:如圖,已知![]() ,射線
,射線![]() 在
在![]() 外部,且
外部,且![]() .若射線
.若射線![]() 平分
平分![]() .求
.求![]() 的度數.
的度數.
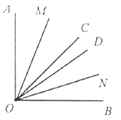
![]() :如圖,已知
:如圖,已知![]() ,射線
,射線![]() 在
在![]() 的內部,射線
的內部,射線![]() 在
在![]() 的內部,且
的內部,且![]() ,若射線
,若射線![]() 平分
平分![]() ,射線
,射線![]() 平分
平分![]() .求
.求![]() 的度數.
的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A,B,C,D,E,F為⊙O的六等分點,動點P從圓心O出發,沿OE弧EFFO的路線做勻速運動,設運動的時間為t,∠BPD的度數為y,則下列圖象中表示y與t之間函數關系最恰當的是( )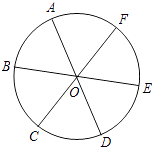
A.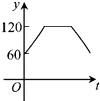
B.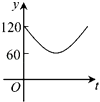
C.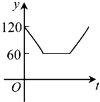
D.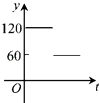
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料:
在數學課上,老師請同學思考如下問題:
請利用直尺和圓規確定圓中弧AB所在圓的圓心![]()
小亮的作法如下:
如圖:
① 在弧AB上任意取一點C,分別連接AC,BC
②分別作AC,BC的垂直平分線,兩條垂線平分線交于O點,所以點O就是所求弧AB的圓心
老師說:“小亮的作法正確.”
請你回答:小亮的作圖依據是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直線a∥b,直線c分別與直線a,b相交于點E,F,點A,B分別在直線a,b上,且在直線c的左側,點P是直線c上一動點(不與點E,F重合),設∠PAE=∠1,∠APB=∠2,∠PBF=∠3.
(1)如圖,當點P在線段EF上運動時,試探索∠1,∠2,∠3之間的關系,并給出證明;
(2)當點P在線段EF外運動時,請你在備用圖中畫出圖形,并判斷(1)中的結論是否還成立?若不成立,請你探索∠1,∠2,∠3之間的關系(不需要證明).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com