
【題目】如圖,四邊形ABCD中,AD∥BC,∠A=90°,AD=1cm,AB=3cm,BC=5cm,動點P從點B出發以1cm/s的速度沿BC的方向運動,動點Q從點C出發以2cm/s的速度沿CD方向運動,P、Q兩點同時出發,當Q到達點D時停止運動,點P也隨之停止,設運動的時間為ts(t>0)
(1)求線段CD的長;
(2)t為何值時,線段PQ將四邊形ABCD的面積分為1:2兩部分?

【答案】(1)5厘米;(2)當t為 ![]() 秒時,線段PQ將四邊形ABCD的面積分為1:2兩部分.
秒時,線段PQ將四邊形ABCD的面積分為1:2兩部分.
【解析】
(1)作DE⊥BC于E,則四邊形ADEB是矩形,在直角△DEC中運用勾股定理即可求解;
(2)由題意可知BP=t厘米,則PC=(5﹣t)厘米,CQ=2t厘米,同時由題意可知0<t≤2.5;作QH⊥BC于點H,運用三角形相似可求解QH的長度表達式,則可列出△DEC的面積表達式,再按線段PQ將四邊形ABCD的面積分為1:2兩部分,分S△PQC:S四邊形ABCD=1:3和S△PQC:S四邊形ABCD=2:3兩種情況分別討論.
(1)解:如圖1,作DE⊥BC于E,則四邊形ADEB是矩形.
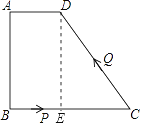
∴BE=AD=1,DE=AB=3,
∴EC=BC﹣BE=4,
在Rt△DEC中,DE2+EC2=DC2 ,
∴DC= ![]() =5厘米;
=5厘米;
(2)解:∵點P的速度為1厘米/秒,點Q的速度為2厘米/秒,運動時間為t秒,
∴BP=t厘米,PC=(5﹣t)厘米,CQ=2t厘米,QD=(5﹣2t)厘米,
且0<t≤2.5,
作QH⊥BC于點H,
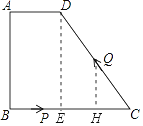
∴DE∥QH,
∴∠DEC=∠QHC,
∵∠C=∠C,
∴△DEC∽△QHC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴QH= ![]() t,
t,
∴S△PQC= ![]() PCQH=
PCQH= ![]() (5﹣t)
(5﹣t) ![]() t=﹣
t=﹣ ![]() t2+3t,
t2+3t,
S四邊形ABCD= ![]() (AD+BC)AB=
(AD+BC)AB= ![]() (1+5)×3=9,
(1+5)×3=9,
分兩種情況討論:
①當S△PQC:S四邊形ABCD=1:3時,
﹣ ![]() t2+3t=
t2+3t= ![]() ×9,即t2﹣5t+5=0,
×9,即t2﹣5t+5=0,
解得t1= ![]() ,t2=
,t2=![]() (舍去);
(舍去);
②S△PQC:S四邊形ABCD=2:3時,
﹣ ![]() t2+3t=
t2+3t= ![]() ×9,即t2﹣5t+10=0,
×9,即t2﹣5t+10=0,
∵△<0,
∴方程無解,
∴當t為 ![]() 秒時,線段PQ將四邊形ABCD的面積分為1:2兩部分.
秒時,線段PQ將四邊形ABCD的面積分為1:2兩部分.


科目:初中數學 來源: 題型:
【題目】一列快車由甲地開往乙地,一列慢車由乙地開往甲地,兩車同時出發,勻速運動,快車離乙地的路程![]() (
(![]() )與行駛的時間
)與行駛的時間![]() (
(![]() )之間的函數關系,如圖中線段
)之間的函數關系,如圖中線段![]() 所示,慢車離乙地的路程
所示,慢車離乙地的路程![]() (
(![]() )與行駛的時間
)與行駛的時間![]() (
(![]() )之間的函數關系,如圖中線段
)之間的函數關系,如圖中線段![]() 所示,則快、慢車相距225
所示,則快、慢車相距225![]() 時,行駛的時間是( )
時,行駛的時間是( )

A.1![]() B.3
B.3![]() C.1
C.1![]() 或3
或3![]() D.2
D.2![]() 或4
或4![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,![]() ,
,![]() 的平分線與BC的延長線交于點E,與DC交于點F,且點F為邊DC的中點,
的平分線與BC的延長線交于點E,與DC交于點F,且點F為邊DC的中點,![]() ,垂足為G,若
,垂足為G,若![]() ,則AE的邊長為
,則AE的邊長為![]()
![]()

A. ![]() B.
B. ![]() C. 4 D. 8
C. 4 D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學習小組由3名男生和1名女生組成,在一次合作學習后,開始進行成果展示.
(1)如果隨機抽取1名同學單獨展示,那么女生展示的概率為 ;
(2)如果隨機抽取2名同學共同展示,求同為男生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
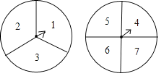
【題目】兩個自由轉動的轉盤如圖所示,一個分為![]() 等份,分別標有數字
等份,分別標有數字![]() ,
,![]() ,
,![]() ,另一個分為
,另一個分為![]() 等份,分別標有數字
等份,分別標有數字![]() ,
,![]() ,
,![]() ,
,![]() .轉盤上有固定指針,同時轉動兩個轉盤,當轉盤停止轉動后,指針指向的數字即為轉出的數字.甲、乙兩人制定游戲規則如下:一人先猜數,然后另一人再轉動轉盤,若猜出的數字與轉出的兩個數字之和相等,則猜數的人獲勝,否則轉動轉盤的人獲勝.猜數者可從下面
.轉盤上有固定指針,同時轉動兩個轉盤,當轉盤停止轉動后,指針指向的數字即為轉出的數字.甲、乙兩人制定游戲規則如下:一人先猜數,然后另一人再轉動轉盤,若猜出的數字與轉出的兩個數字之和相等,則猜數的人獲勝,否則轉動轉盤的人獲勝.猜數者可從下面![]() ,
,![]() 兩種方案中選一種:方案
兩種方案中選一種:方案![]() :猜“奇數”或猜“偶數”其中的一種;方案
:猜“奇數”或猜“偶數”其中的一種;方案![]() :猜“是
:猜“是![]() 的整數倍”或猜“不是
的整數倍”或猜“不是![]() 的整數倍”其中的一種.
的整數倍”其中的一種.
![]() 如果你是猜數的游戲者,為了盡可能獲勝,你將選擇哪種方案,猜該種方案中的哪一種情況?請說明理由;
如果你是猜數的游戲者,為了盡可能獲勝,你將選擇哪種方案,猜該種方案中的哪一種情況?請說明理由;
![]() 為了保證參與游戲雙方的公平性,你應選擇哪種猜數的方案?為什么?
為了保證參與游戲雙方的公平性,你應選擇哪種猜數的方案?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,PA,PB是⊙O的兩條切線,A,B為切點,直線OP交⊙O于C,D,交AB于E,AF為⊙O的直徑,下列結論中正確的有:①∠ABP=∠AOP;②AP=BP;③弧BC=弧DF ;④∠APO=∠BPO;⑤AB⊥PD.
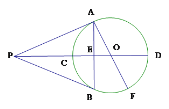
A. ①⑤ B. ②③⑤ C. ①④ D. ①②③④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知在△ABC中,AB=AC,D是△ABC外接圓劣弧AC上的點(不與A,C重合),延長BD至E.
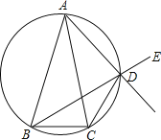
(1)求證:AD的延長線平分∠CDE;
(2)若∠BAC=30°,且△ABC底邊BC邊上高為1,求△ABC外接圓的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將兩個全等的直角三角尺ABC和ADE如圖擺放,∠CAB=∠DAE=90°,∠ACB=∠DEA=30°,使點D落在BC邊上,連結EB,EC,則下列結論:①∠DAC=∠DCA;②ED為AC的垂直平分線;③EB平分∠AED;④△ACE為等邊三角形.其中正確的是( )
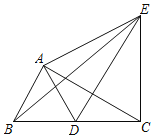
A.①②③B.①②④C.②③④D.①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(2017甘肅省天水市)△ABC和△DEF是兩個全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的頂點E與△ABC的斜邊BC的中點重合,將△DEF繞點E旋轉,旋轉過程中,線段DE與線段AB相交于點P,線段EF與射線CA相交于點Q.
(1)如圖①,當點Q在線段AC上,且AP=AQ時,求證:△BPE≌△CQE;
(2)如圖②,當點Q在線段CA的延長線上時,求證:△BPE∽△CEQ;并求當BP=2,CQ=9時BC的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com