
【題目】已知:如圖,邊長為2的正五邊形ABCDE內接于⊙O,AB、DC的延長線交于點F,過點E作EG∥CB交BA的延長線于點G.

(1)求證: ![]() ;
;
(2)證明:EG與⊙O相切,并求AG、BF的長.
【答案】(1)見解析;(2)見解析
【解析】試題分析:欲證AB2=AGBF,可證△EAG∽△FBC及正五邊形ABCDE的特點得出;求AG、BF的長,需連接EF,易證明EF⊥BC,得出EF⊥EG,依據EG與⊙O相切,用切線的性質得出.
試題解析:證明:(1)易證五邊形ABCDE的外角∠FCB=∠EAG=∠FBC,
∵EG∥CB,
∴∠EAG=∠FBC.
∴△EAG∽△FBC.
∴![]() ,即BCAE=AGBF.
,即BCAE=AGBF.
又∵BC=AE=AB,
∴![]() .①
.①
(2)連接EF,由(1)可知FB=FC,即△FBC為等腰三角形,易知BA=CD,

∴FA=FD,
∴EF⊥BC且EF平分BC,
∴EF過圓心O.
又∵EG∥CB,∴EF⊥EG,
∴EG與⊙O相切.
∴![]() .
.
由(1)可知∠G=∠EAG,∴EG=EA=2,
設AG=x,則![]() ,解得
,解得![]()
∴AG=![]() ,代入①中可得:BF=
,代入①中可得:BF=![]() .
.


科目:初中數學 來源: 題型:
【題目】當三角形中一個內角是另一個內角的3倍時,我們稱此三角形為“夢想三角形”.如果一個“夢想三角形”有一個角為108°,那么這個“夢想三角形”的最小內角的度數為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題滿分10分)如圖,已知直線![]() 和雙曲線
和雙曲線![]() (k>0),點A(m,n)在雙曲線
(k>0),點A(m,n)在雙曲線 ![]() 上.當m=n=2時.
上.當m=n=2時.
(1)直接寫出k的值;
(2)將直線![]() 作怎樣的平移能使平移后的直線與雙曲線
作怎樣的平移能使平移后的直線與雙曲線 ![]() 只有一個交點.
只有一個交點.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,△DEF是由△ABC繞點O順時針旋轉180°后形成的圖形;
(1)請你指出圖中所有相等的線段;
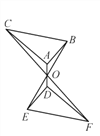
(2)圖中哪些三角形可以被看成是關于點O成中心對稱關系?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)拋物線![]() 經過點A (4,0),點B (1,-3) ,求該拋物線的解析式;
經過點A (4,0),點B (1,-3) ,求該拋物線的解析式;
(2)如圖,要修建一個圓形噴水池,在池中心豎直安裝一根水管,在水管的頂端安一個噴水頭,使噴出的拋物線形水柱在與池中心的水平距離為1m處達到最高,高度為3m,水柱落地處離池中心3m,水管應多長?

(3)如圖,點P![]() (
(![]() >0),在
>0),在![]() 軸正半軸上,過點P作平行于
軸正半軸上,過點P作平行于![]() 軸的直線,分別交拋物線
軸的直線,分別交拋物線![]() 于點A,B,交拋物線
于點A,B,交拋物線![]() 于點C,D,求
于點C,D,求![]() 的值.
的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線![]() 與
與![]() 軸交于點A,點B(1,0),與
軸交于點A,點B(1,0),與![]() 軸交于點C(0,﹣3),點M是其頂點.
軸交于點C(0,﹣3),點M是其頂點.
(1)求拋物線解析式;
(2)第一象限拋物線上有一點D,滿足∠DAB=45°,求點D的坐標;
(3)直線![]() (﹣3<
(﹣3<![]() <﹣1)與x軸相交于點H.與線段AC,AM和拋物線分別相交于點E,F,P.證明線段HE,EF,FP總能組成等腰三角形.
<﹣1)與x軸相交于點H.與線段AC,AM和拋物線分別相交于點E,F,P.證明線段HE,EF,FP總能組成等腰三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
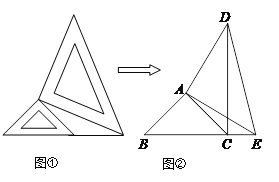
【題目】兩個大小不同的等腰直角三角板如圖①所示放置,圖②是由它抽象出來的幾何圖形,點B、C、E在同一條直線上,連結DC.
(1)請找出圖②中的全等三角形,并給予證明;
(2)求證:DC⊥BE.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com