【題目】如圖，AC⊥BC，DC⊥EC，AC=BC，DC=EC，圖中AE、BD有怎樣的關系（數量關系和位置關系）？并證明你的結論．
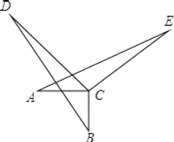
【答案】結論：AE=BD，AE⊥BD，證明見解析.
【解析】
只要證明△DCB≌△ECA（SAS），推出∠A=∠B，BD=AE由∠AND=∠BNC，∠B+∠BNC=90°推出∠A+∠AND=90°，可得∠AON=90°由此即可解決問題．
結論：AE=BD，AE⊥BD．理由如下：
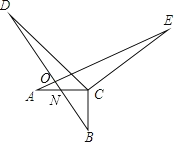
如圖，設AC交BD于N，AE交BD于O．
∵AC⊥BC，DC⊥EC，∴∠ACB=∠DCE=90°，∴∠DCB=∠ECA．
在△DCB和△ECA中，∵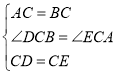
，∴△DCB≌△ECA（SAS），∴∠A=∠B，BD=AE．
∵∠AND=∠BNC，∠B+∠BNC=90°，∴∠A+∠AND=90°，∴∠AON=90°，∴BD⊥AE．
培優口算題卡系列答案
開心口算題卡系列答案
口算題卡河北少年兒童出版社系列答案科目：初中數學 來源： 題型：
【題目】某市為了節約生活用水，計劃制定每位居民統一的月用水量標準，然后根據標準，實行分段收費．為此，對居民上年度的月均用水量進行了抽樣調查，并根據調查結果繪制了上年度月均用水量的頻數分布直方圖(圖中分組含最低值，不含最高值)，請根據圖中信息解答下列問題：
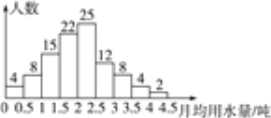
(1)本次調查的居民人數為__________人；
(2)本次調查的居民月均用水量的中位數落在頻數分布直方圖中的第__________小組內(從左至右數)；
(3)當地政府希望讓85%左右居民的月均用水量低于制定的月用水量標準，根據上述調查結果，你認為月用水量標準(取整數)定為多少噸時較為合適？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，在△ABC中，AB=AC，AD⊥BC，垂足為點D，AN是△ABC外角∠CAM的平分線，CE⊥AN，垂足為點E，
(1)求證：四邊形ADCE為矩形；
(2)當△ABC滿足什么條件時，四邊形ADCE是一個正方形？并給出證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】“賞中華詩詞，尋文化基因，品生活之美”，某校舉辦了首屆“中國詩詞大會”，經選拔后有50名學生參加決賽，這50名學生同時默寫50首古詩詞，若每正確默寫出一首古詩詞得2分，根據測試成績繪制出部分頻數分布表和部分頻數分布直方圖如圖表.
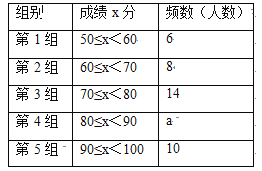
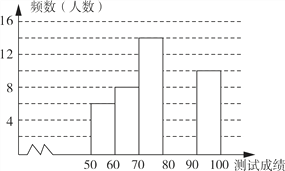
請結合圖表完成下列各題：
（1）① 表中a的值為 ；
② 把頻數分布直方圖補充完整；
（2）若測試成績不低于80分為優秀，則本次測試的優秀率是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】計算:
（1）a a3a5
（2）（x6）2+（x3）4+x12
（3）
（4）(-3a2b3)(-2ab3c)3
（5）
（6）(x+2)(x-3)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）如圖1，AB∥CD，∠A=35°，∠C=40°，求∠APC的度數．（提示：作PE∥AB）．
（2）如圖2，AB∥DC，當點P在線段BD上運動時，∠BAP=∠α，∠DCP=∠β，求∠CPA與∠α，∠β之間的數量關系，并說明理由．
（3）在（2）的條件下，如果點P在射線DM上運動，請你直接寫出∠CPA與∠α，∠β之間的數量關系______．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在ABCD中，E，F分別為邊AB，CD的中點，BD是對角線．
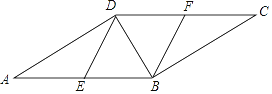
（1）求證：△ADE≌△CBF；
（2）若∠ADB是直角，請證明四邊形BEDF是菱形．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
