
 已知:如圖,四邊形ABCD是關于坐標原點中心對稱的四邊形,其中點A(1,3),B(3,1),反比例函數=
已知:如圖,四邊形ABCD是關于坐標原點中心對稱的四邊形,其中點A(1,3),B(3,1),反比例函數= 經過點A.
經過點A.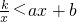 的解集為:______.
的解集為:______. 得k=1×3=3,
得k=1×3=3,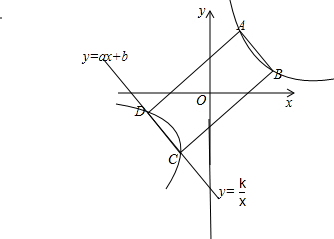
 ;
; 得圖象上,
得圖象上, 的交點,
的交點,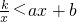 .
. 可求出k,從而得到反比例函數解析式;
可求出k,從而得到反比例函數解析式; 得圖象上,然后觀察函數圖象得到當x<-3或-1<x<0時,一次函數圖象都在反比例函數圖象上方,由此可得到不等式
得圖象上,然后觀察函數圖象得到當x<-3或-1<x<0時,一次函數圖象都在反比例函數圖象上方,由此可得到不等式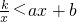 的解集.
的解集.

科目:初中數學 來源: 題型:
 已知:如圖,四邊形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四邊形ABCD繞直線AB旋轉一周,則所得幾何體的表面積是多少?
已知:如圖,四邊形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四邊形ABCD繞直線AB旋轉一周,則所得幾何體的表面積是多少?查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com