
【題目】已知拋物線![]() 與直線
與直線![]() 有兩個不同的交點.下列結論:①
有兩個不同的交點.下列結論:①![]() ;②當
;②當![]() 時,
時,![]() 有最小值
有最小值![]() ;③方程
;③方程![]() 有兩個不等實根;④若連接這兩個交點與拋物線的頂點,恰好是一個等腰直角三角形,則
有兩個不等實根;④若連接這兩個交點與拋物線的頂點,恰好是一個等腰直角三角形,則![]() ;其中正確的結論的個數是( )
;其中正確的結論的個數是( )
A.4B.3C.2D.1
【答案】B
【解析】
根據“拋物線![]() 與直線
與直線![]() 有兩個不同的交點”即可判斷①③;根據拋物線的對稱軸為直線x=1即可判斷②;根據等腰直角三角形的性質,用c表達出兩個交點,代入拋物線解析式計算即可判斷④.
有兩個不同的交點”即可判斷①③;根據拋物線的對稱軸為直線x=1即可判斷②;根據等腰直角三角形的性質,用c表達出兩個交點,代入拋物線解析式計算即可判斷④.
解:∵拋物線![]() 與直線
與直線![]() 有兩個不同的交點,
有兩個不同的交點,
∴![]() 有兩個不相等的實數根,即
有兩個不相等的實數根,即![]() 有兩個不相等的實數根,故③正確,
有兩個不相等的實數根,故③正確,
∴![]() ,解得:
,解得:![]() ,故①正確;
,故①正確;
∵拋物線的對稱軸為直線x=1,且拋物線開口向上,
∴當x=1時,![]() 為最小值,故②正確;
為最小值,故②正確;
若連接這兩個交點與拋物線的頂點,恰好是一個等腰直角三角形,
則頂點(1,c-2)到直線y=2的距離等于兩交點距離的一半,
∵頂點(1,c-2)到直線y=2的距離為2-(c-2)=4-c,
∴兩交點的橫坐標分別為1-(4-c)=c-3與1+(4-c)=5-c
∴兩交點坐標為(c-3,2)與(5-c,2),
將(c-3,2)代入![]() 中得:
中得:![]()
解得:![]() 或
或![]()
∵![]() ,
,
∴![]() ,故④錯誤,
,故④錯誤,
∴正確的有①②③,
故選:B.


科目:初中數學 來源: 題型:
【題目】已知反比例函數的圖象經過三個點A(﹣4,﹣3),B(2m,y1),C(6m,y2),其中m>0.
(1)當y1﹣y2=4時,求m的值;
(2)如圖,過點B、C分別作x軸、y軸的垂線,兩垂線相交于點D,點P在x軸上,若三角形PBD的面積是8,請寫出點P坐標(不需要寫解答過程).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2015年是中國人民抗日戰爭暨世界反法西斯戰爭勝利70周年,9月3日全國各地將舉行有關紀念活動.為了解初中學生對二戰歷史的知曉情況,某初中課外興趣小組在本校學生中開展了專題調查活動,隨機抽取了部分學生進行問卷調查,根據學生的答題情況,將結果分為![]() 、
、![]() 、
、![]() 、
、![]() 四類,其中
四類,其中![]() 類表示“非常了解”,
類表示“非常了解”,![]() 類表示“比較了解”,
類表示“比較了解”,![]() 類表示“基本了解”;
類表示“基本了解”;![]() 類表示“不太了解”,調查的數據經整理后形成尚未完成的條形統計圖(如圖①)和扇形統計圖(如圖②):
類表示“不太了解”,調查的數據經整理后形成尚未完成的條形統計圖(如圖①)和扇形統計圖(如圖②):
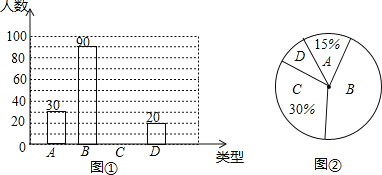
(1)在這次抽樣調查中,一共抽查了 名學生;
(2)請把圖①中的條形統計圖補充完整;
(3)圖②的扇形統計圖中![]() 類部分所對應扇形的圓心角的度數為 ;
類部分所對應扇形的圓心角的度數為 ;
(4)如果這所學校共有初中學生1500名,請你估算該校初中學生中對二戰歷史“非常了解”和“比較了解”的學生共有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為迎接”抗戰勝利70周年紀念展”,中國國家博物館進行了合并改擴建工程.新館的展廳總面積與原館大樓的總建筑面積相同,成為目前世界上最大的博物館.已知原館大樓的總建筑面積比原館大樓的展覽面積的3倍少0.4萬平方米,新館的展廳總面積比原館大樓的展覽面積大4.2萬平方米,求新館的展廳總面積和原館大樓的展覽面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線y=﹣x2+bx+c(b,c為常數)與x軸交于點(x1,0)和(x2,0),與y軸交于點A,點E為拋物線頂點.
(Ⅰ)當x1=﹣1,x2=3時,求點E,點A的坐標;
(Ⅱ)①若頂點E在直線y=x上時,用含有b的代數式表示c;
②在①的前提下,當點A的位置最高時,求拋物線的解析式;
(Ⅲ)若x1=﹣1,b>0,當P(1,0)滿足PA+PE值最小時,求b的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() 中,
中,![]() 是
是![]() 邊上的一點,
邊上的一點,![]() ,
,![]() 是
是![]() 的外接圓,
的外接圓,![]() 是
是![]() 的直徑,且交
的直徑,且交![]() 于點
于點![]() .
.
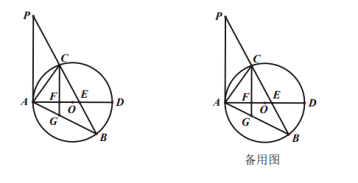
(1)求證: ![]() 是
是![]() 的切線;
的切線;
(2)過點![]() 作
作![]() 于點
于點![]() ,延長
,延長![]() 交
交![]() 于點
于點![]() 若
若![]() 求
求![]() 的長;
的長;
(3)在滿足(2)的條件下,若![]() 求
求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 問題發現
問題發現
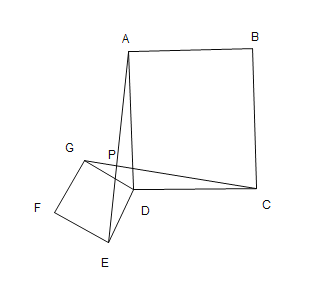
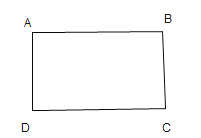
如圖![]() ,正方形
,正方形![]() 將正方形
將正方形![]() 繞點
繞點![]() 旋轉,直線
旋轉,直線![]() 交于點
交于點![]() 請直接寫出線段
請直接寫出線段![]() 與
與![]() 的數量關系是 ,位置關系是 _;
的數量關系是 ,位置關系是 _;
![]() 拓展探究
拓展探究
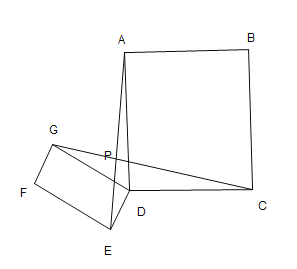
如圖![]() ,矩形
,矩形![]() 將矩形
將矩形![]() 繞點
繞點![]() 旋轉,直線
旋轉,直線![]() 交于點
交于點![]()
![]() 中線段關系還成立嗎/若成立,請寫出理由;若不成立,請寫出線段
中線段關系還成立嗎/若成立,請寫出理由;若不成立,請寫出線段![]() 的數量關系和位置關系,并說明理由;
的數量關系和位置關系,并說明理由;
![]() 解決問題
解決問題
在![]() 的條件下,
的條件下,![]() 矩形
矩形![]() 繞
繞![]() 點旋轉過程中,請直接寫出當點
點旋轉過程中,請直接寫出當點![]() 與點
與點![]() 重合時,線段
重合時,線段![]() 的長,
的長,
查看答案和解析>>
科目:初中數學 來源: 題型:
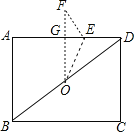
【題目】如圖,在矩形ABCD中,AB=6,BC=8,點O為對角線BD的中點,點E為邊AD上一點,連接OE,將△DOE沿OE翻折得到△OEF,若OF⊥AD于點G,則OE=______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com