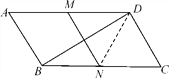
【題目】如圖，在平行四邊形ABCD中，∠C＝60°，M、N分別是AD、BC的中點，BC＝2CD.
(1)求證：四邊形MNCD是平行四邊形；
(2)求證：BD＝
MN.
【答案】見解析
【解析】試題分析：（1）要證明四邊形MNCD是平行四邊形，即要證明MD＝NC，MD∥NC，由四邊形ABCD是平行四邊形可得AD＝BC，AD∥BC，又因為M、N分別是AD、BC的中點，所以MD＝NC，MD∥NC；（2）連結ND，由四邊形MNCD是平行四邊形可得 MN＝DC，因為N是BC的中點，所以BN＝CN，結合BC＝2CD，∠C＝60°可以得出△NCD是等邊三角形，進而得出ND＝NC，∠DNC＝60°，由三角形外角的性質可得∠NBD＋∠NDB＝∠DNC，
因為DN＝NC＝NB，所以∠DBN＝∠BDN＝
∠DNC＝30°，所以∠BDC＝90°，最后結合tan∠DBC可證明DB＝
MN.
試題解析：
(1)∵四邊形ABCD是平行四邊形，∴AD＝BC，AD∥BC，
∵M、N分別是AD、BC的中點，∴MD＝NC，MD∥NC，
∴四邊形MNCD是平行四邊形；
(2)連結ND，
∵四邊形MNCD是平行四邊形，∴MN＝DC，
∵N是BC的中點，∴BN＝CN，
∵BC＝2CD，∠C＝60°，∴△NCD是等邊三角形，∴ND＝NC，∠DNC＝60°，
∵∠DNC是△BND的外角，∴∠NBD＋∠NDB＝∠DNC，
∵DN＝NC＝NB，∴∠DBN＝∠BDN＝∠DNC＝30°，∴∠BDC＝90°，
∵tan∠DBC＝tan30°＝
＝
，
∴DB＝DC＝MN.
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，點Q為坐標系上任意一點，某圖形上的所有點在∠Q的內部（含角的邊），這時我們把∠Q的最小角叫做該圖形的視角．如圖1，矩形ABCD，作射線OA，OB，則稱∠AOB為矩形ABCD的視角． 
（1）如圖1，矩形ABCD，A（﹣ 
，1），B（ ，1），C（ ，3），D（﹣ ，3），直接寫出視角∠AOB的度數；
（2）在（1）的條件下，在射線CB上有一點Q，使得矩形ABCD的視角∠AQB=60°，求點Q的坐標；
（3）如圖2，⊙P的半徑為1，點P（1， ），點Q在x軸上，且⊙P的視角∠EQF的度數大于60°，若Q（a，0），求a的取值范圍． 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在邊長為1的小正方形組成的網格中，△AOB的三個頂點均在格點上，點A、B的坐標分別為(3，2)、(1，3)．△AOB繞點O逆時針旋轉90后得到△A1OB1．
（1）在網格中畫出△A1OB1，并標上字母；
（2）點A關于O點中心對稱的點的坐標為___________；
（3）點A1的坐標為________；
（4）△A1OB1的面積為_______________.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小明在學習二次根式后，發現一些含根號的式子可以寫成另一個式子的平方，如3＋2
＝(1＋
)2，善于思考的小明進行了以下探索：
設a＋b
＝(m＋n
)2(其中a、b、m、n均為正整數)，則有a＋b
＝m2＋2n2＋2mn
，
∴a＝m2＋2n2，b＝2mn.這樣小明就找到了一種把a＋b
的式子化為平方式的方法．
請你仿照小明的方法探索并解決下列問題：
（1）當a、b、m、n均為正整數時，若a＋b
＝(m＋n
)2，用含m、n的式子分別表示a、b，得：a＝ , b＝ .
（2）利用所探索的結論，找一組正整數a、b、m、n填空： + = ( + )2；(答案不唯一)
（3）若a＋4
＝(m＋n
)2 ,且a、m、n均為正整數,求a的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為加強中小學生安全和禁毒教育，某校組織了“防溺水、交通安全、禁毒”知識競賽，為獎勵在競賽中表現優異的班級，學校準備從體育用品商場一次性購買若干個足球和籃球（每個足球的價格相同，每個籃球的價格相同），購買1個足球和1個籃球共需159元；足球單價是籃球單價的2倍少9元．
（1）求足球和籃球的單價各是多少元？
（2）根據學校實際情況，需一次性購買足球和籃球共20個，但要求購買足球和籃球的總費用不超過1550元，學校最多可以購買多少個足球？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，A，B兩點在數軸上對應的數分別為a，b，且點A在點B的左邊，|a|=10，a+b=80，ab＜0．
(1)求出a，b的值；
(2)現有一只電子螞蟻P從點A出發，以3個單位長度/秒的速度向右運動，同時另一只電子螞蟻Q從點B出發，以2個單位長度/秒的速度向左運動．
①設兩只電子螞蟻在數軸上的點C相遇，求出點C對應的數是多少？
②經過多長時間兩只電子螞蟻在數軸上相距20個單位長度？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
