
(本題滿分10分)如圖,直線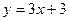 交
交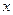 軸于A點,交
軸于A點,交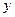 軸于B點,過A、B兩點的拋物線交
軸于B點,過A、B兩點的拋物線交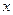 軸于另一點C(3,0)
軸于另一點C(3,0) .
.
⑴求拋物線的解析式;
⑵在拋物線的對稱軸上是否存在點Q,使△ABQ是等腰三角形?若存在,求出符合條件的Q點坐標;若不存在,請說明理由.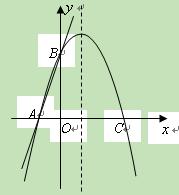
解:(1)∵當 =0時,
=0時, =3
=3
當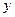 =0時,
=0時,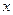 =﹣1
=﹣1
∴ (﹣1,0),
(﹣1,0), (0,3)
(0,3)
∵ (3,0)··························1分
(3,0)··························1分
設拋物線的解析式為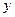 =a(
=a(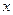 +1)(
+1)(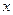 ﹣3)
﹣3)
∴3=a×1×(﹣3)
∴a=﹣1
∴此拋物線的解析式為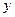 =﹣(
=﹣(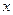 + 1)(
+ 1)(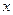 ﹣3)=-
﹣3)=-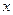
 +2
+2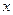 +3·····2分
+3·····2分
(2)存在∵拋物線的對稱軸為:= =1···············4分
=1···············4分
∴如圖對稱軸與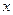 軸的交點即為Q
軸的交點即為Q
∵ =
=
 ,
, ⊥
⊥

∴ =
=


∴
 (1,0)··························6分
(1,0)··························6分
當

 =
=

 時,設
時,設
 的坐標為(1,m)
的坐標為(1,m)
∴2 +m
+m =1
=1 +(3﹣m)
+(3﹣m)
∴m=1
∴
 (1,1)··························8分
(1,1)··························8分
當

 =
= 時,設
時,設
 (1,n)
(1,n)
∴2 +n
+n =1
=1 +3
+3
∵n>0 ∴n= ∴
∴
 (1,
(1, )
)
∴符合條件的 點坐標為
點坐標為
 (1,0),
(1,0),
 (1,1),
(1,1),
 (1,
(1, )·10分
)·10分
解析


科目:初中數學 來源: 題型:
(本題滿分10分)
如圖,將OA = 6,AB = 4的矩形OABC放置在平面直角坐標系中,動點M、N以每秒1個單位的速度分別從點A、C同時出發,其中點M沿AO向終點O運動,點N沿CB向終點B運動,當兩個動點運動了t秒時,過點N作NP⊥BC,交OB于點P,連接MP.

(1)點B的坐標為 ;用含t的式子表示點P的坐標為 ;(3分)
(2)記△OMP的面積為S,求S與t的函數關系式(0 < t < 6);并求t為何值時,S有最大值?(4分)
(3)試探究:當S有最大值時,在y軸上是否存在點T,使直線MT把△ONC分割成三角形和四邊形兩部分,且三角形的面積是△ONC面積的?若存在,求出點T的坐標;若不存在,請說明理由.(3分)
查看答案和解析>>
科目:初中數學 來源: 題型:
 的圖象的頂點為
的圖象的頂點為 .二次函數
.二次函數 的圖象與
的圖象與 軸交于原點
軸交于原點 及另一點
及另一點 ,它的頂點
,它的頂點 在函數
在函數 的圖象的對稱軸上.
的圖象的對稱軸上.
 與點
與點 的坐標;
的坐標; 為菱形時,求函數
為菱形時,求函數 的關系式.
的關系式.查看答案和解析>>
科目:初中數學 來源: 題型:
 與支架
與支架 所在直線相交于水箱橫斷面
所在直線相交于水箱橫斷面 的圓心
的圓心 ,支架
,支架 與水平面
與水平面 垂直,
垂直, 厘米,
厘米,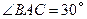 ,另一根輔助支架
,另一根輔助支架 厘米,
厘米, .
. 的長度;(結果保留根號)
的長度;(結果保留根號) 的長度.(結果保留三個有效數字,參考數據:
的長度.(結果保留三個有效數字,參考數據: )
)

查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源:2011年江蘇省泰州市中考數學試卷 題型:解答題
(本題滿分10分)如圖,以點O為圓心的兩個同心圓中,矩形ABCD的邊BC為大圓的弦,邊AD與小圓相切于點M,OM的延長線與BC相交于點N。
(1)點N是線段BC的中點嗎?為什么?
(2)若圓環的寬度(兩圓半徑之差)為6cm,AB=5cm,BC=10cm,求小圓的半徑。

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com