
【題目】如圖,在等邊三角形ABC右側作射線CP,∠ACP=![]() (0°<
(0°<![]() <60°),點A關于射線CP的對稱點為點D,BD交CP于點E,連接AD,AE.
<60°),點A關于射線CP的對稱點為點D,BD交CP于點E,連接AD,AE.

(1)求∠DBC的大小(用含![]() 的代數式表示);
的代數式表示);
(2)在![]() (0°<
(0°<![]() <60°)的變化過程中,∠AEB的大小是否發生變化?如果發生變化,請直接寫出變化的范圍;如果不發生變化,請直接寫出∠AEB的大小;
<60°)的變化過程中,∠AEB的大小是否發生變化?如果發生變化,請直接寫出變化的范圍;如果不發生變化,請直接寫出∠AEB的大小;
(3)用等式表示線段AE,BD,CE之間的數量關系,并證明.
【答案】(1)∠DBC![]() ;(2)∠AEB的大小不會發生變化,且∠AEB=60°;(3)BD=2AE+CE,證明見解析.
;(2)∠AEB的大小不會發生變化,且∠AEB=60°;(3)BD=2AE+CE,證明見解析.
【解析】
(1)如圖1,連接CD,由軸對稱的性質可得AC=DC,∠DCP=∠ACP=![]() ,由△ABC是等邊三角形可得AC=BC,∠ACB=60°,進一步即得∠BCD=
,由△ABC是等邊三角形可得AC=BC,∠ACB=60°,進一步即得∠BCD=![]() ,BC=DC,然后利用三角形的內角和定理即可求出結果;
,BC=DC,然后利用三角形的內角和定理即可求出結果;
(2)設AC、BD相交于點H,如圖2,由軸對稱的性質可證明△ACE≌△DCE,可得∠CAE=∠CDE,進而得∠DBC=∠CAE,然后根據三角形的內角和可得∠AEB=∠BCA,即可作出判斷;
(3)如圖3,在BD上取一點M,使得CM=CE,先利用三角形的外角性質得出∠BEC![]() ,進而得△CME是等邊三角形,可得∠MCE=60°,ME=CE,然后利用角的和差關系可得∠BCM=∠DCE,再根據SAS證明△BCM≌△DCE,于是BM=DE,進一步即可得出線段AE,BD,CE之間的數量關系.
,進而得△CME是等邊三角形,可得∠MCE=60°,ME=CE,然后利用角的和差關系可得∠BCM=∠DCE,再根據SAS證明△BCM≌△DCE,于是BM=DE,進一步即可得出線段AE,BD,CE之間的數量關系.
解:(1)如圖1,連接CD,∵點A關于射線CP的對稱點為點D,∴AC=DC,∠DCP=∠ACP=![]() ,
,
∵△ABC是等邊三角形,∴AC=BC,∠ACB=60°,
∴∠BCD=![]() ,BC=DC,
,BC=DC,
∴∠DBC=∠BDC![]() ;
;
(2)∠AEB的大小不會發生變化,且∠AEB=60°.
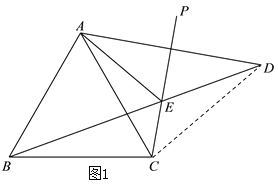
理由:設AC、BD相交于點H,如圖2,∵點A關于射線CP的對稱點為點D,
∴AC=DC,AE=DE,又∵CE=CE,∴△ACE≌△DCE(SSS),∴∠CAE=∠CDE,
∵∠DBC=∠BDC,∴∠DBC=∠CAE,又∵∠BHC=∠AHE,∴∠AEB=∠BCA=60°,
即∠AEB的大小不會發生變化,且∠AEB=60°;
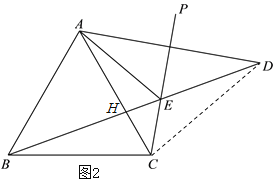
(3)AE,BD,CE之間的數量關系是:BD=2AE+CE.
證明:如圖3,在BD上取一點M,使得CM=CE,
∵∠BEC=∠BDC+∠DCE=![]() ,
,
∴△CME是等邊三角形,∴∠MCE=60°,ME=CE,
∴![]() ,
,
∴∠BCM=∠DCE,又∵BC=DC,CM=CE,
∴△BCM≌△DCE(SAS),∴BM=DE,
∵AE=DE,
∴BD=BM+ME+DE=2DE+ME=2AE+CE.
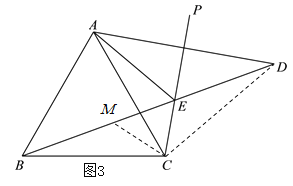


科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,AC=BC,點O是斜邊AB的中點,將邊長足夠大的三角板的直角頂點放在點O處,將三角板繞點O順時針旋轉一個角度α(0°<α<90°),記三角板的兩直角邊與Rt△ABC的兩腰AC、BC的交點分別為E、D,四邊形CEOD是旋轉過程中三角板與△ABC的重疊部分(如圖①所示).那么,在上述旋轉過程中:

(1)線段CE與BD具有怎樣的數量關系?四邊形CEOD的面積是否發生變化?證明你發現的結論;
(2)當三角尺旋轉角度為____________時,四邊形CEOD是矩形;
(3)若三角尺繼續旋轉,當旋轉角度α(90°<α<180°)時,三角尺的兩邊與等腰Rt△ABC的腰CB和AC的延長線分別交于點D、E(如圖②所示). 那么線段CE與BD的數量關系還成立嗎?若成立,給予證明;若不成立,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】分別畫出滿足下列條件的點:(尺規作圖,請保留作圖痕跡,不寫作法.作圖痕跡請加粗加黑!)
(1)在邊![]() 上找一點
上找一點![]() ,使
,使![]() 到
到![]() 和
和![]() 的距離相等;
的距離相等;
(2)在射線![]() 上找一點
上找一點![]() ,使
,使![]() .
.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=![]() x2-4x+7與y=
x2-4x+7與y=![]() x交于A、B兩點(點A在點B左側).
x交于A、B兩點(點A在點B左側).
(1)求A、B兩點坐標;
(2)求拋物線頂點C的坐標,并求△ABC面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() 經過點
經過點![]() 和點
和點![]() ,且
,且![]() .
.

![]() 如圖,若
如圖,若![]() 點恰好是拋物線的頂點,請寫出它的對稱軸和
點恰好是拋物線的頂點,請寫出它的對稱軸和![]() 的值.
的值.
![]() 若
若![]() ,求
,求![]() 、
、![]() 的值,并指出此時拋物線的開口方向.
的值,并指出此時拋物線的開口方向.
![]() 若拋物線
若拋物線![]() 的開口向下,請直接寫出
的開口向下,請直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年10月1日,慶祝中華人民共和國成立![]() 周年大會在京隆重舉行.當天在天安門廣場舉行了盛大閱兵式和群眾游行,閱兵式的全體受閱官兵由人民解放軍、武警部隊和民兵預備役部隊約
周年大會在京隆重舉行.當天在天安門廣場舉行了盛大閱兵式和群眾游行,閱兵式的全體受閱官兵由人民解放軍、武警部隊和民兵預備役部隊約![]() 名官兵、
名官兵、![]() 臺(套)裝備組成的
臺(套)裝備組成的![]() 個徒步方隊、
個徒步方隊、![]() 個裝備方隊;陸海、空航空兵
個裝備方隊;陸海、空航空兵![]() 余架戰機組成的
余架戰機組成的![]() 個空中梯隊和
個空中梯隊和![]() 個空中護旗隊根據上述數據繪制了以下尚不完整的統計圖表:
個空中護旗隊根據上述數據繪制了以下尚不完整的統計圖表:

根據圖表提供的信息,解答以下問題:
(1)統計表中的![]() ;
;![]() .
.
(2)請補全條形統計圖;

(3)在閱兵過程中,已知直播介紹空中護旗隊為![]() 秒,介紹每個徒步方隊裝備方隊、空中梯隊經過的時間分別為
秒,介紹每個徒步方隊裝備方隊、空中梯隊經過的時間分別為![]() 秒、
秒、![]() 秒、
秒、![]() 秒,請你求出每個方(護旗梯)隊的平均播出時間.
秒,請你求出每個方(護旗梯)隊的平均播出時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,AC是弦,∠BAC的平分線交⊙O于點D,過點D作DE⊥AC交AC的延長線于點E,連接BD。

(1)求證:DE是⊙O的切線;
(2)若tan∠ABD=2,CE=1,求⊙O的半徑。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=x2-(m+3)x+9的頂點C在x軸正半軸上,一次函數y=x+3與拋物線交于A、B兩點,與x、y軸分別交于D、E兩點.
(1)求m的值;
(2)求A、B兩點的坐標.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com