
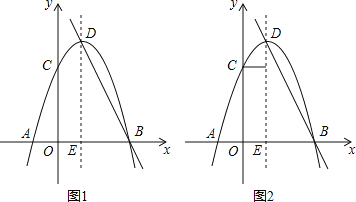
【題目】關于x的一元二次方程(m+1)x2+2(m+1)x+2=0有兩個相等的實數根,拋物線y=﹣x2+(m+1)x+3與x軸交于A、B兩點(A在B左側),與y軸相交于點C,拋物線的頂點為D.
(1)求拋物線的解析式.
(2)如圖1,設拋物線的對軸交x軸于點E,在拋物線的對稱軸上是否存在點P,使P點到x軸的距離等于P點到直線BD的距離?若存在,求出點P的坐標,若不存在,請說明理由.
(3)如圖2,作CF⊥DE于F,M為射線EA上一動點.如果在線段EF上恰好存在兩個點N滿足△CFN與△NEM相似,求M點的坐標.
【答案】(1)y=﹣x2+2x+3.(2)當點P坐標為(2,![]() ﹣1)或(2,﹣
﹣1)或(2,﹣![]() ﹣1)時,P點到x軸的距離等于P點到直線BD的距離.(3)
﹣1)時,P點到x軸的距離等于P點到直線BD的距離.(3)![]()
【解析】
(1)利用根的判別式列式求解即可.(2)由題意可知,點P在∠DBE及其外角的角平分線上,則角平分線與對稱軸的交點,即為點P的位置,利用勾股定理求解即可.(3)當以CM為直徑的⊙K與EF相切時,恰好存在兩個點N,使得△MNE和△CFN相似,由此確定M的位置,設EM=a,連接KN,則KN是梯形CFEM的中位線,則KN=![]() ,CM=1+a,在Rt△CMO中,利用勾股定理列方程求解即可.
,CM=1+a,在Rt△CMO中,利用勾股定理列方程求解即可.
解:(1)∵一元二次方程(m+1)x2+2(m+1)x+2=0有兩個相等的實數根,
∴△=0且m+1≠0,
∴4(m+1)2﹣4(m+1)×2=0,
解得m=±1,
∵m≠﹣1,
∴m=1,
∴拋物線解析式為y=﹣x2+2x+3.
(2)存在.如圖1中,
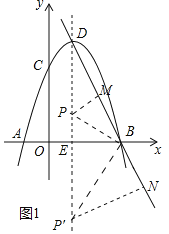
①當P在x軸上方時,作PM⊥BD,設PM=PE=m,
由題意可知A(﹣1,0),B(3,0),D(1,4),
∴DE=4,BE=2,BD=![]() =
=![]() =2
=2![]() ,
,
在Rt△PDM中,∵PD2=DM2=PM2,
∴(4﹣m)2=(2![]() ﹣2)2+m2,
﹣2)2+m2,
解得m=![]() ﹣1,
﹣1,
∴此時點P坐標(2,![]() ﹣1).
﹣1).
②當P′在x軸下方時,作P′N⊥BD于N.設P′N=P′E=m,
在Rt△DP′N中,∵P′D2=DN2+P′N2,
∴(4+m)2=(2![]() +2)2+m2,
+2)2+m2,
解得m=![]() +1,
+1,
∴此時點P′坐標(2,﹣![]() ﹣1).
﹣1).
綜上所述,當點P坐標為(2,![]() ﹣1)或(2,﹣
﹣1)或(2,﹣![]() ﹣1)時,P點到x軸的距離等于P點到直線BD的距離.
﹣1)時,P點到x軸的距離等于P點到直線BD的距離.
(3)如圖2中,當以CM為直徑的⊙K與EF相切時,恰好存在兩個點N,使得△MNE和△CFN相似.
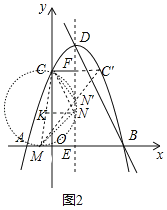
①設切點為N,則∠CNM=90°,
∵∠CFN=∠MEN=90°,
∴∠MNE+∠CNF=90°,∠CNF+∠NCF=90°,
∴∠MNE=∠NCF,
∴△MNE∽△NCF.
②作C關于直線DE的對稱點C′,連接MC′交DE于N′,
∵∠CN′F=∠C′N′F=∠MN′E,∠CFN′=∠MEN′=90°,
∴△N′ME∽△N′CF.
∴當以CM為直徑的⊙K與EF相切時,恰好存在兩個點N,使得△MNE和△CFN相似,
設EM=a,連接KN,則KN是梯形CFEM的中位線,
∴KN=![]() ,CM=1+a,
,CM=1+a,
在Rt△CMO中,∵CM2=CO2+OM2,
∴(1+a)2=(a﹣1)2=32,
解得a=![]() ,
,
∴OM=EM﹣OE=![]() ﹣1=
﹣1=![]() ,
,
∴點M坐標為(﹣![]() ,0).
,0).


科目:初中數學 來源: 題型:
【題目】某數學興趣小組對函數y=![]() 的圖象和性質進行探究,他們用描點法畫此函數圖象時,先列表如下
的圖象和性質進行探究,他們用描點法畫此函數圖象時,先列表如下
(1)請補全此表;
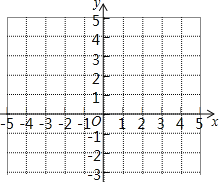
(2)根據表中數據,在如圖坐標系中畫出該函數的圖象;
(3)請寫出此函數圖象不同方面的三個性質;
(4)若點(m,y1),(2,y2)都在此函數圖象上,且y1≤y2,求m的取值范圍
x | …… | _____ | ____ | _____ | _____ | 0 | 1 | 2 | 3 | 4 | …… |
y | …… | _____ | ____ | _____ | _____ | 4 | 2 |
|
|
|
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在銳角△ABC中,AB=4,BC=5,∠ACB=45°,將△ABC繞點B按逆時針方向旋轉,得到△A1BC1.
(1)如圖1,當點C1在線段CA的延長線上時,求∠CC1A1的度數;
(2)如圖2,連接AA1,CC1.若△ABA1的面積為4,求△CBC1的面積;
(3)如圖3,點E為線段AB中點,點P是線段AC上的動點,在△ABC繞點B按逆時針方向旋轉過程中,點P的對應點是點P1,求線段EP1長度的最大值與最小值.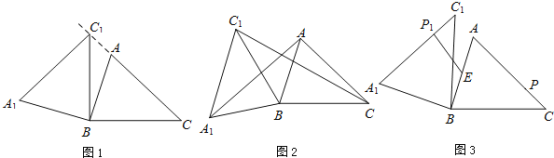
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為增強學生的身體素質,教育行政部門規定學生每天參加戶外活動的平均時間不少于1小時.為了解學生參加戶外活動的情況,對部分學生參加戶外活動的時間進行抽樣調查,并將調查結果繪制作成如下兩幅不完整的統計圖,請你根據圖中提供的信息解答下列問題:
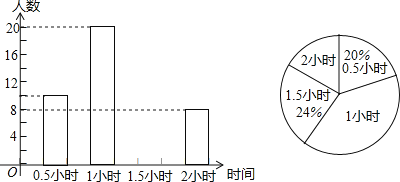
(1)在這次調查中共調查了多少名學生?
(2)補充頻數分布直方圖;
(3)求表示戶外活動時間 1小時的扇形圓心角的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
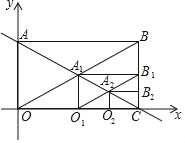
【題目】如圖,直線y=![]() 與x軸y軸分別交于A、C兩點,以AC為對角線作第一個矩形ABCO,對角線交點為A1,再以CA1為對角線作第二個矩形A1B1CO1,對角線交點為A2,同法作第三個矩形A2B2CO2對角線交點為A3,…以此類推,則第2019個矩形對角線交點A2019的坐標為_____.
與x軸y軸分別交于A、C兩點,以AC為對角線作第一個矩形ABCO,對角線交點為A1,再以CA1為對角線作第二個矩形A1B1CO1,對角線交點為A2,同法作第三個矩形A2B2CO2對角線交點為A3,…以此類推,則第2019個矩形對角線交點A2019的坐標為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
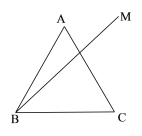
【題目】如圖,等邊△ABC中,BM是ABC內部的一條射線,且![]() ,點A關于BM的對稱點為D,連接AD,BD,CD,其中AD、CD的延長線分別交射線BM于點E,P.
,點A關于BM的對稱點為D,連接AD,BD,CD,其中AD、CD的延長線分別交射線BM于點E,P.
(1)依題意補全圖形;
(2)若ABM ,求BDC 的大小(用含的式子表示);
(3)用等式表示線段PB,PC與PE之間的數量關系,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題再現:
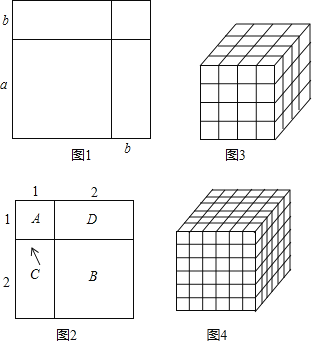
數形結合是解決數學問題的一種重要的思想方法,借助這種方法可將抽象的數學知識變得直觀起來并且具有可操作性,從而可以幫助我們快速解題.初中數學里的一些代數公式,很多都可以通過表示幾何圖形面積的方法進行直觀推導和解釋.例如:利用圖形的幾何意義推證完全平方公式.將一個邊長為a的正方形的邊長增加b,形成兩個矩形和兩個正方形,如圖1,這個圖形的面積可以表示成:(a+b)2或a2+2ab+b2∴(a+b)2=a2+2ab+b2
這就驗證了兩數和的完全平方公式.
問題提出:
如何利用圖形幾何意義的方法推證:13+23=32 如圖2,A表示1個1×1的正方形,即:1×1×1=13,B表示1個2×2的正方形,C與D恰好可以拼成1個2×2的正方形,因此:B、C、D就可以表示2個2×2的正方形,即:2×2×2=23,而A、B、C、D恰好可以拼成一個(1+2)×(1+2)的大正方形,由此可得:13+23=(1+2)2=32
嘗試解決:
請你類比上述推導過程,利用圖形幾何意義方法推證:13+23+33= (要求自己構造圖形并寫出推證過程)
類比歸納:
請用上面的表示幾何圖形面積的方法探究:13+23+33+…+n3= (要求直接寫出結論,不必寫出解題過程)
實際應用:
圖3是由棱長為1的小正方體搭成的大正方體,圖中大小正方體一共有多少個?為了正確數出大小正方體的總個數,我們可以分類統計,即分別數出棱長是1,2,3和4的正方體的個數,再求總和.
例如:棱長是1的正方體有:4×4×4=43個,棱長是2的正方體有:3×3×3=33個,棱長是3的正方體有:2×2×2=23個,棱長是4的正方體有:1×1×l=13個,然后利用(3)類比歸納的結論,可得: = 圖4是由棱長為1的小正方體成的大正方體,圖中大小正方體一共有 個.
逆向應用:
如果由棱長為1的小正方體搭成的大正方體中,通過上面的方式數出的大小正方體一共有44100個,那么棱長為1的小正方體一共有 個.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com