
【題目】如圖1,在平面直角坐標系![]() 中,直線AB與
中,直線AB與![]() 軸交于點A、與
軸交于點A、與![]() 軸交于點B,且∠ABO=45°,A(-6,0),直線BC與直線AB關于
軸交于點B,且∠ABO=45°,A(-6,0),直線BC與直線AB關于![]() 軸對稱.
軸對稱.
(1)求△ABC的面積;
(2)如圖2,D為OA延長線上一動點,以BD為直角邊,D為直角頂點,作等腰直角△BDE,求證:AB⊥AE;
(3)如圖3,點E是![]() 軸正半軸上一點,且∠OAE=30°,AF平分∠OAE,點M是射線AF上一動點,點N是線段AO上一動點,判斷是否存在這樣的點M,N,使OM+NM的值最小?若存在,請寫出其最小值,并加以說明.
軸正半軸上一點,且∠OAE=30°,AF平分∠OAE,點M是射線AF上一動點,點N是線段AO上一動點,判斷是否存在這樣的點M,N,使OM+NM的值最小?若存在,請寫出其最小值,并加以說明.



【答案】(1)36;(2)證明見解析;(3)3,理由見解析.
【解析】
(1)根據直線與坐標軸的交點易得A,C的坐標,從而得出AC=12,OB=6,根據三角形面積公式可求解;
(2) 過E作EF⊥x軸于點F,延長EA交y軸于點H,證△DEF≌△BDO,得出EF=OD=AF,有![]() ,得出∠BAE=90°.
,得出∠BAE=90°.
(3)由已知條件可在線段OA上任取一點N,再在AE作關于OF的對稱點![]() ,當點N運動時,
,當點N運動時,![]() 最短為點O到直線AE的距離.再由
最短為點O到直線AE的距離.再由![]() ,在直角三角形
,在直角三角形![]() 中,
中,![]()
即可得解.
解:(1)由已知條件得:
AC=12,OB=6
∴![]()
(2)過E作EF⊥x軸于點F,延長EA交y軸于點H,

∵△BDE是等腰直角三角形,
∴DE=DB, ∠BDE=90°,
∴![]()
∵![]()
∴![]()
∴![]()
∵EF![]() 軸,
軸,
∴![]()
∴DF=BO=AO,EF=OD
∴AF=EF
∴![]()
∴∠BAE=90°
(3)由已知條件可在線段OA上任取一點N,再在AE作關于OF的對稱點![]() ,當點N運動時,
,當點N運動時,![]() 最短為點O到直線AE的距離,即點O到直線AE的垂線段的長,
最短為點O到直線AE的距離,即點O到直線AE的垂線段的長,

∵![]() ,OA=6,
,OA=6,
∴OM+ON=3


 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案科目:初中數學 來源: 題型:
【題目】閱讀下面材料:
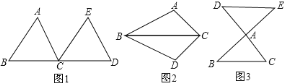
如圖![]() ,把
,把![]() 沿直線
沿直線![]() 平行移動線段
平行移動線段![]() 的長度,可以變到
的長度,可以變到![]() 的位置;
的位置;
如圖![]() ,以
,以![]() 為軸,把
為軸,把![]() 翻折
翻折![]() ,可以變到
,可以變到![]() 的位置;
的位置;
如圖![]() ,以點
,以點![]() 為中心,把
為中心,把![]() 旋轉
旋轉![]() ,可以變到
,可以變到![]() 的位置.
的位置.
像這樣,其中一個三角形是由另一個三角形按平行移動、翻折、旋轉等方法變成的.這種只改變位置,不改變形狀大小的圖形變換,叫做三角形的全等變換.
回答下列問題:
①在圖![]() 中,可以通過平行移動、翻折、旋轉中的哪一種方法怎樣變化,使
中,可以通過平行移動、翻折、旋轉中的哪一種方法怎樣變化,使![]() 變到
變到![]() 的位置;
的位置;
②指圖中線段![]() 與
與![]() 之間的關系,為什么?
之間的關系,為什么?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC的面積為1.第一次操作:分別延長AB,BC,CA至點A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,順次連結A1,B1,C1,得到△A1B1C1.第二次操作:分別延長A1B1,B1C1,C1A1至點A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,順次連結A2,B2,C2,得到△A2B2C2.…按此規律,要使得到的三角形的面積超過2013,最少經過_____次操作.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC,且∠ABC=60°,D為△ABC內一點 ,且DA=DB,E為△ABC外一點,BE=AB,且∠EBD=∠CBD,連DE,CE. 下列結論:①∠DAC=∠DBC;②BE⊥AC ;③∠DEB=30°. 其中正確的是( )

A.①...B.①③...C.② ...D.①②③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一座建于若干年前的水庫大壩的橫斷面如圖所示,其中背水面的整個坡面是長為![]() 米、寬為
米、寬為![]() 米的矩形.現需將其整修并進行美化,方案如下:①將背水坡
米的矩形.現需將其整修并進行美化,方案如下:①將背水坡![]() 的坡度由
的坡度由![]() 改為
改為![]() ;②用一組與背水坡面長邊垂直的平行線將背水坡面分成
;②用一組與背水坡面長邊垂直的平行線將背水坡面分成![]() 塊相同的矩形區域,依次相間地種草與栽花.
塊相同的矩形區域,依次相間地種草與栽花.

(1)求整修后背水坡面的面積;
(2)如果栽花的成本是每平方米![]() 元,種草的成本是每平方米
元,種草的成本是每平方米![]() 元,那么種植花草至少需要多少元?
元,那么種植花草至少需要多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“萬州古紅桔”原名“萬縣紅桔”,古稱丹桔(以下簡稱為紅桔),種植距今至少已有一千多年的歷史,“玫瑰香橙”(源自意大利西西里島塔羅科血橙,以下簡稱香橙)現已是萬州柑橘發展的主推品種之一.某水果店老板在2017年11月份用15200元購進了400千克紅桔和600千克香橙,已知香橙的每千克進價比紅桔的每千克進價2倍還多4元.
(1)求11月份這兩種水果的進價分別為每千克多少元?
(2)時下正值柑橘銷售旺季,水果店老板決定在12月份繼續購進這兩種水果,但進入12月份,由于柑橘的大量上市,紅桔和香橙的進價都有大幅下滑,紅桔每千克的進價在11月份的基礎上下降了![]() m%,香橙每千克的進價在11月份的基礎上下降了m%,由于紅桔和“玫瑰香橙”都深受庫區人民歡迎,實際水果店老板在12月份購進的紅桔數量比11月份增加了
m%,香橙每千克的進價在11月份的基礎上下降了m%,由于紅桔和“玫瑰香橙”都深受庫區人民歡迎,實際水果店老板在12月份購進的紅桔數量比11月份增加了![]() m%,香橙購進的數量比11月份增加了2m%,結果12月份所購進的這兩種柑橘的總價與11月份所購進的這兩種柑橘的總價相同,求m的值.
m%,香橙購進的數量比11月份增加了2m%,結果12月份所購進的這兩種柑橘的總價與11月份所購進的這兩種柑橘的總價相同,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ACB中,∠ACB=90゜,CD⊥AB于D.

(1)求證:∠ACD=∠B;
(2)若AF平分∠CAB分別交CD、BC于E、F,求證:∠CEF=∠CFE.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC=10cm,BC=6cm,點D為AB的中點.如果點P在線段BC上以1cm/s的速度由點B向點C運動,同時點Q在線段CA上由點C向點A運動.

(1)若點Q的運動速度與點P的運動速度相等,經過1秒,△BPD與△CQP是否全等?請說明理由;
(2)若點Q的運動速度與點P的運動速度不相等,當點Q的運動速度為多少時,能夠使△BPD與△CQP全等?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com