
 、
、 分別在
分別在 軸、
軸、 軸的正半軸上,且
軸的正半軸上,且 ,點
,點 為線段
為線段 的中點.
的中點. 的長度為________________;
的長度為________________;
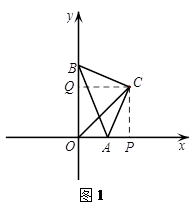
 為斜邊作等腰直角三角形
為斜邊作等腰直角三角形 ,當點
,當點 在第一象限時,求直線
在第一象限時,求直線 所對應的函數的解析式;
所對應的函數的解析式;
 、
、 分別在
分別在 軸、
軸、 軸的負半軸上,且
軸的負半軸上,且 ,以
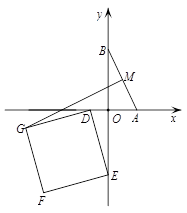
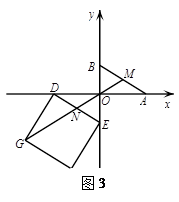
,以 為邊在第三象限內作正方形
為邊在第三象限內作正方形 ,請求出線段
,請求出線段 長度的最大值,并直接寫出此時直線
長度的最大值,并直接寫出此時直線 所對應的函數的解析式.
所對應的函數的解析式.
|
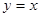 (3)線段MG取最大值10+
(3)線段MG取最大值10+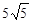 .
.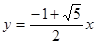
 的長度為5.
的長度為5. 為斜邊作等腰直角三角形
為斜邊作等腰直角三角形 ,當點
,當點 在第一象限時,過點C分別作CP⊥x軸于P,CQ⊥y軸于Q.
在第一象限時,過點C分別作CP⊥x軸于P,CQ⊥y軸于Q.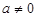 ).
).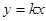 ,
,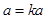 ,解得k=1,所以直線OC所對應的函數解析式為
,解得k=1,所以直線OC所對應的函數解析式為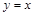 (3)取DE的中點N,連結ON、NG、OM.因為∠AOB=90°,所以OM=
(3)取DE的中點N,連結ON、NG、OM.因為∠AOB=90°,所以OM= .同理得ON=5.
.同理得ON=5. .在點M與G之間總有
.在點M與G之間總有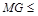 MO+ON+NG由于∠DNG的大小為定值,只要
MO+ON+NG由于∠DNG的大小為定值,只要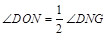 ,且M、N關于點O中心對稱時,M、O、N、G四點共線,此時等號成立.這時線段MG取最大值10+
,且M、N關于點O中心對稱時,M、O、N、G四點共線,此時等號成立.這時線段MG取最大值10+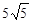 .
.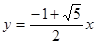

 在第一象限,
在第一象限,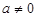 ).
).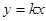 ,
,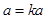 ,解得k=1,
,解得k=1,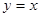 . 4分
. 4分 .
.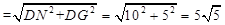 .
.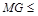 MO+ON+NG(如圖2),
MO+ON+NG(如圖2),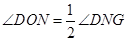 ,且M、N關于點O中心對稱時,M、O、N、G四點共線,此時等號成立(如圖3).
,且M、N關于點O中心對稱時,M、O、N、G四點共線,此時等號成立(如圖3).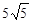 .
.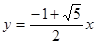


 特高級教師點撥系列答案
特高級教師點撥系列答案科目:初中數學 來源:不詳 題型:解答題
 和直線y=kx+b交于A,B兩點,點A的坐標為(﹣3,2),BC⊥y軸于點C,且OC=6BC.
和直線y=kx+b交于A,B兩點,點A的坐標為(﹣3,2),BC⊥y軸于點C,且OC=6BC.
 的解集.
的解集.查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題


查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
| x(單位:臺) | 10 | 20 | 30 |
| y(單位:萬元∕臺) | 60 | 55 | 50 |

查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
 上的一點,過點M作x軸、y軸的垂線,分別交直線
上的一點,過點M作x軸、y軸的垂線,分別交直線 于D、C兩點,若直線
于D、C兩點,若直線 與y軸交于點A,與x軸相交于點B.則AD•BC的值為 .
與y軸交于點A,與x軸相交于點B.則AD•BC的值為 .
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com