
【題目】如圖1,在平面直角坐標系中,點![]() ,點
,點![]() ,以
,以![]() 為邊在右側作正方形
為邊在右側作正方形![]()

(1)當點![]() 在
在![]() 軸正半軸上運動時,求點
軸正半軸上運動時,求點![]() 的坐標(用
的坐標(用![]() 表示);
表示);
(2)當![]() 時,如圖2,
時,如圖2,![]() 為
為![]() 上一點,過點
上一點,過點![]() 作
作![]() ,
,![]() ,連
,連![]() 交
交![]() 于點
于點![]() ,求
,求![]() 的值;
的值;
(3)如圖3,在第(2)問的條件下,![]() 、
、![]() 分別為
分別為![]() 、
、![]() 上的點,作
上的點,作![]() 軸交
軸交![]() 于
于![]() ,作
,作![]() 軸交
軸交![]() 于
于![]() ,
,![]() 是
是![]() 與
與![]() 的交點,若
的交點,若![]() ,試確定
,試確定![]() 的大小,并證明你的結論.
的大小,并證明你的結論.
【答案】(1)C(m+4,m);(2)4![]() ;(3)45°,證明見解析
;(3)45°,證明見解析
【解析】
(1)如圖1中,作CE⊥x軸于E.利用全等三角形的性質即可解決問題;
(2)如圖2中,作ME⊥y軸于E,作MF∥OA交OD于F.構造平行四邊形,全等三角形解決問題即可;
(3)如圖3中,延長CO到M,使得OM=DE.則△AOM≌△ADE.設AG=a,AH=b,由題意DE=a,OF=b,EK=DH=4-b,EC=OG=4-a,利用勾股定理想辦法證明EF=OF+DE=FM,再證明△AFM≌△AFE,可得∠FAM=![]() 即可解決問題.
即可解決問題.
解:(1)如圖1中,作CE⊥x軸于E.
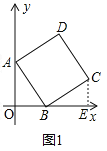
∵∠AOB=∠ABC=∠CEB=90°,
∴∠ABO+∠OAB=90°,∠ABO+∠CBE=90°,
∴∠OAB=∠CBE,∵AB=BC,
∴△ABO≌△BCE,
∴CE=OB=m,BE=OA=4,
∴C(m+4,m).
(2)如圖2中,作ME⊥y軸于E,作MF∥OA交OD于F.
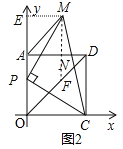
∵∠MEP=∠MPC=∠COP=90°,
∴∠MPE+∠PME=90°,∠MAE+∠CPO=90°,
∴∠PME=∠CPO,∵PM=PC,
∴△MEP≌△OPC,
∴PE=OC=AO,EM=OP,
∴OP=AE=EM,
∴∠EAM=45°,∵∠AOD=45°,
∴∠EAM=∠AOD,
∴AM∥ON,∵OA∥MF,
∴四邊形AMFO是平行四邊形,
∴FM=OA=CD,MF∥CD,AM=OF,
∴∠NDC=∠NFM,∵∠MNF=∠CND,
∴△CDN≌△MFN,
∴FN=DN,
∴AM+2DN=OF+DF=OD=4![]() .
.
(3)如圖3中,延長CO到M,使得OM=DE.則△AOM≌△ADE.
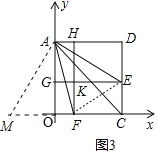
設AG=a,AH=b,由題意DE=a,OF=b,EK=DH=4-b,EC=OG=4-a,
∵S四邊形KFCE=2S四邊形AGKH,
∴(4-a)(4-b)=2ab,
∴16-4(a+b)+ab=2ab,
∴ab=16-4(a+b),
∴2ab=32-8(a+b),
在Rt△EFC中,EF=![]()
∴EF=OF+DE=OF+OM=FM,
∵AF=AF,AM=AE,
∴△AFM≌△AFE,
∴∠FAM=∠FAE,
∵∠DAE=∠OAM,
∴∠EAM=∠DAO=90°,
∴∠EAF=45°.


 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案 優翼小幫手同步口算系列答案
優翼小幫手同步口算系列答案科目:初中數學 來源: 題型:
【題目】如圖,小瑩用一張長方形紙片ABCD進行折紙,已知該紙片寬AB為8cm,BC為10cm.當小瑩折疊時,頂點D落在BC邊上的點F處(折痕為AE).

求(1)BF的長;
(2)EF的長 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】各地“廣場舞”噪音干擾的問題備受關注,相關人員對本地區15~65歲年齡段的500名市民進行了隨機調查,在調查過程中對“廣場舞”噪音干擾的態度有以下五種:A.沒影響;B.影響不大;C.有影響,建議做無聲運動;D.影響很大,建議取締;E.不關心這個問題,將調查結果統計整理并繪制成如下兩幅不完整的統計圖.
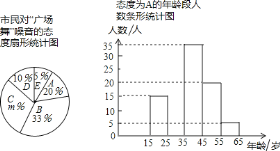
請根據以上信息解答下列問題:
(1)填空m=________,態度為C所對應的圓心角的度數為________;
(2)補全條形統計圖;
(3)若全區15~65歲年齡段有20萬人,估計該地區對“廣場舞”噪音干擾的態度為B的市民人數;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:⊙O為Rt△ABC的外接圓,點D在邊AC上,AD=AO;
(1)如圖1,若弦BE∥OD,求證:OD=BE;
(2)如圖2,點F在邊BC上,BF=BO,若OD=2![]() , OF=3,求⊙O的直徑.
, OF=3,求⊙O的直徑.

查看答案和解析>>
科目:初中數學 來源: 題型:
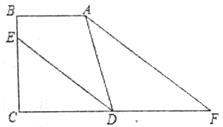
【題目】如圖,AB⊥BC于點B,DC⊥BC于點C,DE平分∠ADC交BC于點E,點F為線段CD延長線上一點,∠BAF=∠EDF.求證:∠DAF=∠F.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有若干個數,第一個記為![]() ,第二個記為
,第二個記為![]() ,第三個記為
,第三個記為![]() …. 若
…. 若![]() ,從第2個數起,每個數都等于“1與它前面那個數的差的倒數”.
,從第2個數起,每個數都等于“1與它前面那個數的差的倒數”.
(1)計算![]() 的值.
的值.
(2)根據以上計算結果,直接寫出![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 三點在數軸上,點
三點在數軸上,點![]() 表示的數是
表示的數是![]() ,從點
,從點![]() 出發向右平移7個單位長度得到點
出發向右平移7個單位長度得到點![]() 。
。
(1)求出點![]() 表示的數,畫一條數軸并在數軸上標出點
表示的數,畫一條數軸并在數軸上標出點![]() 和點
和點![]() ;
;
(2)若此數軸在一張紙上,將紙沿某一條直線對折,此時![]() 點與表示數
點與表示數![]() 的點剛好重合,折痕與數軸有一個交點
的點剛好重合,折痕與數軸有一個交點![]() ,求點
,求點![]() 表示的數的相反數(原卷無此問);
表示的數的相反數(原卷無此問);
(3)在數軸上有一點![]() ,點
,點![]() 到點
到點![]() 和點
和點![]() 的距離之和為11,求點
的距離之和為11,求點![]() 所表示的數;
所表示的數;
(4)![]() 從初始位置分別以1單位長度
從初始位置分別以1單位長度![]() 和2單位長度
和2單位長度![]() 的速度同時向左運動,是否存在
的速度同時向左運動,是否存在![]() 的值,使
的值,使![]() 秒后點
秒后點![]() 到
到![]() 的距離與點
的距離與點![]() 到原點距離相等?若存在請求出
到原點距離相等?若存在請求出![]() 的值;若不存在,請說明理由。
的值;若不存在,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一文體用品商店為吸引中學生顧客,在店內出示了一道數學題,凡是能正確解答這道題的,店內商品一律給該生9折優惠或每購滿10元立減3元(不足10元部分不減)優惠方式.題目是這樣的:購一個筆盒和2個羽毛球共需26元,買2個筆盒和一個羽毛球共需37元,
(1)請列方程或方程組解答商家提出的問題;問:筆盒與羽毛球的單價各是多少元?
(2)一位同學回答對了問題,他想購買羽毛球和筆盒各一個,請列舉能享受到優惠的購買方式,并幫助他選擇一種最優惠的購買方式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙![]() 與菱形
與菱形![]() 在平面直角坐標系中,點
在平面直角坐標系中,點![]() 的坐標為
的坐標為![]() 點
點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 在
在![]() 軸上,且點
軸上,且點![]() 在點
在點![]() 的右側.
的右側.


(![]() )求菱形
)求菱形![]() 的周長.
的周長.
(![]() )若⊙
)若⊙![]() 沿
沿![]() 軸向右以每秒
軸向右以每秒![]() 個單位長度的速度平移,菱形
個單位長度的速度平移,菱形![]() 沿
沿![]() 軸向左以每秒
軸向左以每秒![]() 個單位長度的速度平移,設菱形移動的時間為(
個單位長度的速度平移,設菱形移動的時間為(![]() 秒),當⊙
秒),當⊙![]() 與
與![]() 相切,且切點為
相切,且切點為![]() 的中點時,連接
的中點時,連接![]() ,求
,求![]() 的值及
的值及![]() 的度數.
的度數.
(![]() )在(
)在(![]() )的條件下,當點
)的條件下,當點![]() 與
與![]() 所在的直線的距離為
所在的直線的距離為![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com