
【題目】如圖,直l1∥l2,點A、B固定在直線l2上,點C是直線11上一動點,若點E、F分別為CA、CB中點,對于下列各值:①線段EF的長;②△CEF的周長;③△CEF的面積;④∠ECF的度數,其中不隨點C的移動而改變的是( )

A.①②B.①③C.②④D.③④
【答案】B
【解析】
判斷出AB長為定值,C到AB的距離為定值,再根據三角形的中位線與平行線的性質即可判斷①③,根據運動得出CA+CB不斷發生變化、∠ACB的大小不斷發生變化,即可判斷②④.
解:∵A、B為定點,
∴AB長為定值,
∵點E,F分別為CA,CB的中點,
∴EF是△CAB的中位線,
∴EF=![]() AB為定值,故①正確;
AB為定值,故①正確;
∵點A,B為直線l2上定點,直線l1∥l2,
∴C到l2的距離為定值,
∵EF是△CAB的中位線,
∴EF∥l1∥l2,
∴C到EF的距離為定值,
又∵EF為定值,
∴△CEF的面積為定值,故③正確;
當C點移動時,CA+CB的長發生變化,
則CE+CF的長發生變化,
∴△CEF的周長發生變化,故②錯誤;
當C點移動時,∠ACB發生變化,則∠ECF發生變化,故④錯誤;
故選:B.


科目:初中數學 來源: 題型:
【題目】A,B,C,D四個地區爆發病毒疫情,它們之間的道路連通情況和距離(單位:km)如圖所示,經調查發現,某地區受感染率與相鄰地區自發病率和距離有關,具體公式為:
A地受B地的感染率![]() .已知A地受B地和D地感染率之相鄰地區和為9%,D地的自發病率為24%.
.已知A地受B地和D地感染率之相鄰地區和為9%,D地的自發病率為24%.
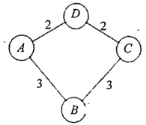
(1)求B地的自發病率;
(2)規定某地的危險系數等于該地的自發病率與總受感染率的和.
①若C地危險系數是A地危險系數的兩倍,且D地受感染率比B地高5%,求A地的自發病率;
②在①的條件下,A地派出6支醫療隊支援B,D兩地,每派出1支醫療隊,A地自身發病率上升0.75%,每支醫療隊可以讓被支援的地區的自發病率下降4%.在保證A地危險系數不上升的前提下,A地各派往B,D兩地多少支隊伍時,B地的自發病率下降最多?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點P為拋物線y![]() x2上一動點,以P為頂點,且經過原點O的拋物線,記作“yp”,設其與x軸另一交點為A,點P的橫坐標為m.
x2上一動點,以P為頂點,且經過原點O的拋物線,記作“yp”,設其與x軸另一交點為A,點P的橫坐標為m.
(1)①當△OPA為直角三角形時,m= ;
②當△OPA為等邊三角形時,求此時“yp”的解析式;
(2)若P點的橫坐標分別為1,2,3,…n(n為正整數)時,拋物線“yp”分別記作“![]() ”、“
”、“![]() ”…,“
”…,“![]() ”,設其與x軸另外一交點分別為A1,A2,A3,…An,過P1,P2,P3,…Pn作x軸的垂線,垂足分別為H1,H2,H3,…Hn.
”,設其與x軸另外一交點分別為A1,A2,A3,…An,過P1,P2,P3,…Pn作x軸的垂線,垂足分別為H1,H2,H3,…Hn.
1)① Pn的坐標為 ;OAn= ;(用含n的代數式來表示)
②當PnHn﹣OAn=16時,求n的值.
2)是否存在這樣的An,使得∠OP4An=90°,若存在,求n的值;若不存在,請說明理由.
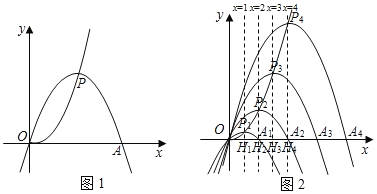
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線y=ax2+bx+c(a≠0)與y軸的交點為A(0,3),與x軸的交點分別為B(2,0),C(6,0).直線AD∥x軸,在x軸上位于點B右側有一動點E,過點E作平行于y軸的直線l與拋物線、直線AD的交點分別為P,Q.
(1)求拋物線的解析式;
(2)當點E在線段BC上時,求△APC面積的最大值;
(3)是否存在點P,使以A,P,Q為頂點的三角形與△AOB相似?若存在,求出此時點E的坐標;若不存在,請說明理由.
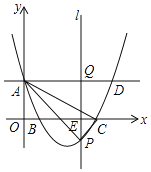
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校舉辦“迎亞運”學生書畫展覽,現要在長方形展廳中劃出3個形狀、大小完全一樣的小長方方形“圖中陰影部分”區域擺放作品.
(1)如圖1,若大長方形的長和寬分別為45米和30米,求小長方形的長和寬;
(2)如圖2,若大長方形的長和寬分別為![]() 和
和![]() .
.
①直接寫出1個小長方形周長與大長方形周長之比;
②若作品展覽區域(陰影部分)面積占展廳面積的![]() ,試求
,試求![]() 的值,
的值,

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形![]() 中,對角線
中,對角線![]() 相交于點
相交于點![]() ,以
,以![]() 為邊向外作等邊
為邊向外作等邊![]() ,連接
,連接![]() 交
交![]() 于
于![]() 若點
若點![]() 為
為![]() 的延長線上一點,連接
的延長線上一點,連接![]() ,連接
,連接![]() 且
且![]() 平分
平分![]() ,下列選項正確的有( )
,下列選項正確的有( )
①![]() ;②
;②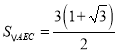 ;③
;③![]() ;④
;④![]()

A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新冠肺炎疫情在全球蔓延,造成了嚴重的人員傷亡和經濟損失,其中一個原因是新冠肺炎病毒傳播速度非常快.一個人如果感染某種病毒,經過了兩輪的傳播后被感染的總人數將達到64人.
(1)求這種病毒每輪傳播中一個人平均感染多少人?
(2)按照上面的傳播速度,如果傳播得不到控制,經過三輪傳播后一共有多少人被感染?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC在平面直角坐標系中的位置如圖,其中每個小正方形的邊長為1個單位長度.
(1)畫出△ABC關于原點O的中心對稱圖形△A1B1C1;
(2)畫出將△ABC繞點C順時針旋轉90°得到△A2B2C2.
(3)在(2)的條件下,求點A旋轉到點A2所經過的路線長(結果保留π).
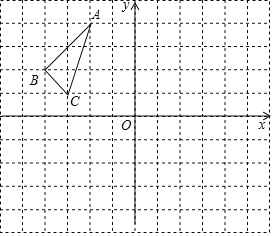
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com