【題目】如圖,在△ABC中, AD是∠BAC的平分線，DF⊥AB，DM⊥AC，垂足分別為F、M，AF=10cm ，BF=6cm ，AC=14cm.動點E以3cm/s的速度從A點向B點運動，動點G以1cm/s的速度從C點向A點運動,當一個點到達終點時,另一個點隨之停止運動,設運動時間為t s.當t=__________s時, △DFE與△DMG全等.(寫出符合題意的t的所有取值)
【答案】3或
【解析】
先根據AB、AC的長、及點E、G的運動速度求出t的取值范圍，再根據角平分線的性質、直角三角形全等的判定定理與性質求出CM的長，然后根據
與
全等，得出
，據此建立方程求解即可．
則點E從點A運動到點B時，運動時間
；點G從點C運動到點A時，運動時間
由題意可得，運動時間t的取值范圍為
是
的平分線，
則點E從點A運動到點F時，運動時間
，此時，點G從點C開始運動的距離為
，即當點E在AF上時，點G一定在CM上
若與全等，則，由題意，分以下3種情況：
（1）當點E在AF上時，
則
，解得
，符合要求
（2）當點E在BF上，點G在CM上時，
則
，解得
，符合要求
（3）當點E在BF上，點G在AM上時，
則
，解得，此時
，不符題意，舍去
綜上，t的值為3或
故答案為：3或．
科目：初中數學 來源： 題型：
【題目】如圖，
個邊長為
的相鄰正方形的一邊均在同一直線上，點
，
，
，…
分別為邊
，
，
，…，
的中點，
的面積為
，
的面積為
，…
的面積為
，則
________．（用含的式子表示）
查看答案和解析>>
科目：初中數學 來源： 題型：
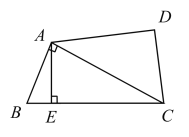
【題目】如圖，小區有一塊四邊形空地
，其中
.為響應沙區創文，美化小區的號召，小區計劃將這塊四邊形空地進行規劃整理.過點
作了垂直于
的小路
.經測量，
，
，
.
（1）求這塊空地的面積；
（2）求小路的長.（答案可含根號）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲、乙兩名同學分別進行6次射擊訓練，訓練成績（單位：環）如下表
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六交 | |
甲 | 9 | 8 | 6 | 7 | 8 | 10 |
乙 | 8 | 7 | 9 | 7 | 8 | 8 |
對他們的訓練成績作如下分析，其中說法正確的是（ ）
A. 他們訓練成績的平均數相同 B. 他們訓練成績的中位數不同
C. 他們訓練成績的眾數不同 D. 他們訓練成績的方差不同
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了從甲、乙兩名選手中選拔出一個人參加射擊比賽，現對他們進行一次測驗，兩個人在相同條件下各射靶10次，為了比較兩人的成績，制作了如下統計圖表．
甲、乙射擊成績統計表
平均數（環） | 中位數（環） | 方差 | 命中10環的次數 |
甲 | 7 | 0 | |
乙 | 1 |
甲、乙射擊成績折線統計圖
（1）請補全上述圖表（請直接在表中填空和補全折線圖）；
（2）如果規定成績較穩定者勝出，你認為誰應勝出？說明你的理由；
（3）如果希望（2）中的另一名選手勝出，根據圖表中的信息，應該制定怎樣的評判規則？為什么？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點P為定角∠AOB的平分線上的一個定點，且∠MPN與∠AOB互補，若∠MPN在繞點P旋轉的過程中，其兩邊分別與OA、OB相交于M、N兩點，則以下結論：（1）PM=PN恒成立；（2）OM+ON的值不變；（3）四邊形PMON的面積不變；（4）MN的長不變，其中正確的個數為（ ）
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，⊙P的圓心是（2，a）（a >0），半徑是2，與y軸相切于點C，直線y=x被⊙P截得的弦AB的長為
，則a的值是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
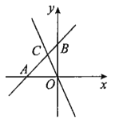
【題目】如圖，在平面直角坐標系中，
為坐標原點．一次函數的圖象與x軸交于點
，與y軸交于點B，與正比例函數
的圖象交于點
．
（1）求一次函數的解析式；
（2）在x軸上尋找點P，使得
為等腰三角形，直接寫出所有滿足條件的點P的坐標；
（3）在直線AB上尋找點Q，使得
，求點Q的坐標．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
