
【題目】已知在△ABC中,AB=AC,∠BAC=α,直線l經過點A(不經過點B或點C),點C關于直線l的對稱點為點D,連接BD,CD.
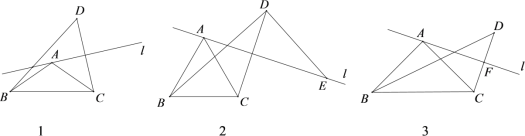
(1)如圖1,
①求證:點B,C,D在以點A為圓心,AB為半徑的圓上;
②直接寫出∠BDC的度數(用含α的式子表示)為 ;
(2)如圖2,當α=60°時,過點D作BD的垂線與直線l交于點E,求證:AE=BD;
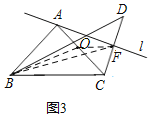
(3)如圖3,當α=90°時,記直線l與CD的交點為F,連接BF.將直線l繞點A旋轉的過程中,在什么情況下線段BF的長取得最大值?若AC=2![]() a,試寫出此時BF的值.
a,試寫出此時BF的值.
【答案】(1)①詳見解析;②![]() α;(2)詳見解析;(3)當B、O、F三點共線時BF最長,(
α;(2)詳見解析;(3)當B、O、F三點共線時BF最長,(![]() +
+![]() )a
)a
【解析】
(1)①由線段垂直平分線的性質可得AD=AC=AB,即可證點B,C,D在以點A為圓心,AB為半徑的圓上;
②由等腰三角形的性質可得∠BAC=2∠BDC,可求∠BDC的度數;
(2)連接CE,由題意可證△ABC,△DCE是等邊三角形,可得AC=BC,∠DCE=60°=∠ACB,CD=CE,根據“SAS”可證△BCD≌△ACE,可得AE=BD;
(3)取AC的中點O,連接OB,OF,BF,由三角形的三邊關系可得,當點O,點B,點F三點共線時,BF最長,根據等腰直角三角形的性質和勾股定理可求![]() ,
,![]() ,即可求得BF
,即可求得BF
(1)①連接AD,如圖1.

∵點C與點D關于直線l對稱,
∴AC = AD.
∵AB= AC,
∴AB= AC = AD.
∴點B,C,D在以A為圓心,AB為半徑的圓上.
②∵AD=AB=AC,
∴∠ADB=∠ABD,∠ADC=∠ACD,
∵∠BAM=∠ADB+∠ABD,∠MAC=∠ADC+∠ACD,
∴∠BAM=2∠ADB,∠MAC=2∠ADC,
∴∠BAC=∠BAM+∠MAC=2∠ADB+2∠ADC=2∠BDC=α
∴∠BDC=![]() α
α
故答案為:![]() α.
α.
(2連接CE,如圖2.
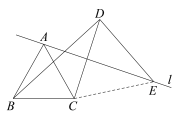
∵∠BAC=60°,AB=AC,
∴△ABC是等邊三角形,
∴BC=AC,∠ACB=60°,
∵∠BDC=![]() α,
α,
∴∠BDC=30°,
∵BD⊥DE,
∴∠CDE=60°,
∵點C關于直線l的對稱點為點D,
∴DE=CE,且∠CDE=60°
∴△CDE是等邊三角形,
∴CD=CE=DE,∠DCE=60°=∠ACB,
∴∠BCD=∠ACE,且AC=BC,CD=CE,
∴△BCD≌△ACE(SAS)
∴BD=AE,
(3)如圖3,取AC的中點O,連接OB,OF,BF,
 ,
,
F是以AC為直徑的圓上一點,設AC中點為O,
∵在△BOF中,BO+OF≥BF,
當B、O、F三點共線時BF最長;
如圖,過點O作OH⊥BC,

∵∠BAC=90°,AB=AC=2![]() a,
a,
∴![]() ,∠ACB=45°,且OH⊥BC,
,∠ACB=45°,且OH⊥BC,
∴∠COH=∠HCO=45°,
∴OH=HC,
∴![]() ,
,
∵點O是AC中點,AC=2![]() a,
a,
∴![]() ,
,
∴![]() ,
,
∴BH=3a,
∴![]() ,
,
∵點C關于直線l的對稱點為點D,
∴∠AFC=90°,
∵點O是AC中點,
∴![]() ,
,
∴![]() ,
,
∴當B、O、F三點共線時BF最長;最大值為(![]() +
+![]() )a.
)a.


科目:初中數學 來源: 題型:
【題目】如圖,在正方形![]() 中,
中,![]() 是
是![]() 邊上一點,連接
邊上一點,連接![]() ,過
,過![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
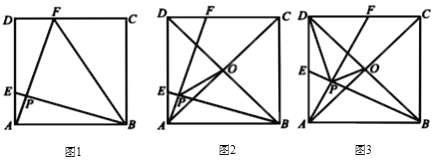
(1)如圖1,連接![]() ,當
,當![]() ,
,![]() 時,求
時,求![]() 的長;
的長;
(2)如圖2,對角線![]() ,
,![]() 交于點
交于點![]() .連接
.連接![]() ,若
,若![]() ,求
,求![]() 的長;
的長;
(3)如圖3,對角線![]() ,
,![]() 交于點
交于點![]() .連接
.連接![]() ,
,![]() ,若
,若![]() ,試探索
,試探索![]() 與
與![]() 的數量關系,并說明理由.
的數量關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() (
(![]() 是常數,
是常數,![]() )的圖象與
)的圖象與![]() 軸交于點
軸交于點![]() 和點
和點![]() (點
(點![]() 在點
在點![]() 的右側),與
的右側),與![]() 軸交于點
軸交于點![]() ,連接
,連接![]() .
.
(1)用含![]() 的代數式表示點
的代數式表示點![]() 和點
和點![]() 的坐標;
的坐標;
(2)垂直于![]() 軸的直線
軸的直線![]() 在點
在點![]() 與點
與點![]() 之間平行移動,且與拋物線和直線
之間平行移動,且與拋物線和直線![]() 分別交于點
分別交于點![]() ,設點
,設點![]() 的橫坐標為
的橫坐標為![]() ,線段
,線段![]() 的長為
的長為![]() .
.
①當![]() 時,求
時,求![]() 的值;
的值;
②若![]() ,則當
,則當![]() 為何值時,
為何值時,![]() 取得最大值,并求出這個最大值.
取得最大值,并求出這個最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() .
.
(1)求拋物線![]() 的開口方向、對稱軸和頂點坐標;
的開口方向、對稱軸和頂點坐標;
(2)將拋物線![]() 向下平移,得拋物線
向下平移,得拋物線![]() ,使拋物線
,使拋物線![]() 的頂點落在直線
的頂點落在直線![]() 上.
上.
①求拋物線![]() 的解析式;
的解析式;
②拋物線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,
,![]() (點
(點![]() 在點
在點![]() 的左側),拋物線
的左側),拋物線![]() 的對稱軸于
的對稱軸于![]() 軸的交點為
軸的交點為![]() ,點
,點![]() 是線段
是線段![]() 上的一點,過點
上的一點,過點![]() 作直線
作直線![]() 軸,交拋物線
軸,交拋物線![]() 于點
于點![]() ,點
,點![]() 關于拋物線對稱軸的對稱點為
關于拋物線對稱軸的對稱點為![]() ,點
,點![]() 是線段
是線段![]() 上一點,且
上一點,且![]() ,連接
,連接![]() ,作
,作![]() 交
交![]() 軸于點
軸于點![]() ,且
,且![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在⊙O中,直徑AB垂直弦CD于E,過點A作∠DAF=∠DAB,過點D作AF的垂線,垂足為F,交AB的延長線于點P,連接CO并延長交⊙O于點G,連接EG.
(1)求證:DF是⊙O的切線;
(2)若AD=DP,OB=3,求![]() 的長度;
的長度;
(3)若DE=4,AE=8,求線段EG的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某旅行團計劃今年暑假組織一個老年人團去昆明旅游,預定賓館住宿時,有住宿條件一樣的甲、乙兩家賓館供選擇,其收費標準為每人每天120元,并且各自推出不同的優惠方案.甲家是35人(含35人)以內的按標準收費,超過35人的,超出部分按九折收費;乙家是45人(含45人)以內的按標準收費,超過45人的,超出部分按八折收費.設老年團的人數為![]() .
.
(1)根據題意,用含有![]() 的式子填寫下表:
的式子填寫下表:
|
|
|
| |
甲賓館收費/元 |
| 5280 | ||
乙賓館收費/元 |
|
| 5400 |
(2)當老年人團的人數為何值時,在甲、乙兩家賓館的花費相同?如果老年人團的人數超過60人,在哪家賓館住宿比較省錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明和爸爸周末步行去游泳館游泳,爸爸先出發了一段時間后小明才出發,途中小明在離家![]() 米處的報亭休息了一段時間后繼續按原來的速度前往游泳館.爸爸、小明離家的距離
米處的報亭休息了一段時間后繼續按原來的速度前往游泳館.爸爸、小明離家的距離![]() (單位:米),
(單位:米),![]() 單位:米)與小明所走時間
單位:米)與小明所走時間![]() (單位:分鐘)之間的函數關系如圖所示,請結合圖象信息解答下列問題:
(單位:分鐘)之間的函數關系如圖所示,請結合圖象信息解答下列問題:

![]() 分別求出爸爸離家的距離
分別求出爸爸離家的距離![]() 和小明到達報亭前離家的距離
和小明到達報亭前離家的距離![]() 與時間
與時間![]() 之間的函數關系式;
之間的函數關系式;
![]() 求小明在報亭休息了多長時間遇到姍姍來遲的爸爸?
求小明在報亭休息了多長時間遇到姍姍來遲的爸爸?
![]() 若游泳館離小明家
若游泳館離小明家![]() 米,請你通過計算說明誰先到達游泳館?
米,請你通過計算說明誰先到達游泳館?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在我們學習過的數學教科書中,有一個數學活動,其具體操作過程是:
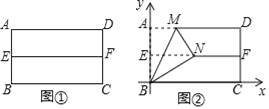
第一步:對折矩形紙片![]() ,使
,使![]() 與
與![]() 重合,得到折痕
重合,得到折痕![]() ,把紙片展開(如圖①);
,把紙片展開(如圖①);
第二步:再一次折疊紙片,使點![]() 落在
落在![]() 上,并使折痕經過點
上,并使折痕經過點![]() ,得到折痕
,得到折痕![]() ,同時得到線段
,同時得到線段![]() (如圖②).
(如圖②).
如圖②所示建立平面直角坐標系,請解答以下問題:
(Ⅰ)設直線![]() 的解析式為
的解析式為![]() ,求
,求![]() 的值;
的值;
(Ⅱ)若![]() 的延長線與矩形
的延長線與矩形![]() 的邊
的邊![]() 交于點
交于點![]() ,設矩形的邊
,設矩形的邊![]() ,
,![]() ;
;
(i)若![]() ,
,![]() ,求
,求![]() 點的坐標;
點的坐標;
(ii)請直接寫出![]() 、
、![]() 應該滿足的條件.
應該滿足的條件.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com