
【題目】四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() 的頂點在
的頂點在![]() 上,
上,![]() 交直線
交直線![]() 于
于![]() 點.
點.
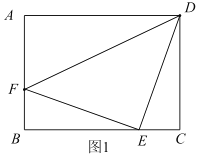

(1)如圖1,若![]() ,
,![]() ,連接
,連接![]() ,求
,求![]() 的長.
的長.
(2)如圖2,![]() ,當
,當![]() 時,求證:
時,求證:![]() 是
是![]() 的中點;
的中點;
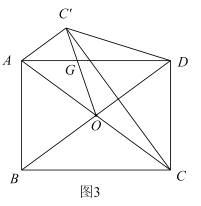
(3)如圖3,若![]() ,對角線
,對角線![]() ,
,![]() 交于點
交于點![]() ,點
,點![]() 關于
關于![]() 的對稱點為點
的對稱點為點![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() 、
、![]() 、
、![]() ,求
,求![]() 的長,請直接寫出答案.
的長,請直接寫出答案.
【答案】(1)![]() ;(2)詳見解析;(3)
;(2)詳見解析;(3)![]() .
.
【解析】
(1)先證明![]() ,求出
,求出![]() ,
,![]() ,利用Rt
,利用Rt![]() 中,求出
中,求出![]() ,再利用等腰直角三角形的性質求出DF的長;
,再利用等腰直角三角形的性質求出DF的長;
(2)在![]() 上取點
上取點![]() ,使
,使![]() ,連接
,連接![]() ,得到
,得到![]() 為等邊三角形,再證明得到
為等邊三角形,再證明得到![]() ,根
,根![]() ,求出
,求出![]() ,故可得到
,故可得到![]() ,即可證明;
,即可證明;
(3)先利用![]() ,得到平行四邊形
,得到平行四邊形![]() 為矩形,設
為矩形,設![]() 與
與![]() 交點為
交點為![]() ,根據對稱性得到OD垂直平分CC’,根據等積法求出CM,利用勾股定理求出OM,再根據中位線的性質求出AC’,利用平行線證明
,根據對稱性得到OD垂直平分CC’,根據等積法求出CM,利用勾股定理求出OM,再根據中位線的性質求出AC’,利用平行線證明![]() ,得到
,得到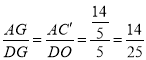 ,再根據AD=8,進而求出AG的長.
,再根據AD=8,進而求出AG的長.
(1)∵![]()
∴∠C=180°-∠B=90°,∠FEB+∠EFB=∠FEB+∠DEC=90°,
∴∠EFB=∠DEC
又![]()
∴![]() ,
,
∴![]()
∵![]()
∴![]() ,
,
在Rt![]() 中,
中,![]()
∵![]() ,
,![]()
∴△DEF是等腰直角三角形,
∴![]() ;
;
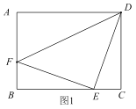
(2)證明:如圖2,在![]() 上取點
上取點![]() ,使
,使![]() ,連接
,連接![]() ,則
,則![]() 為等邊三角形,
為等邊三角形,
∴![]() ,
,
∴![]() .
.
∵四邊形![]() 為平行四邊形,
為平行四邊形,![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∵![]()
∴![]()
∴![]() ,
,![]() ,
,
∴![]() 是
是![]() 的中點.
的中點.
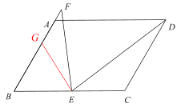
(3)解:由題意得,![]() 為線段
為線段![]() 的垂直平分線,設
的垂直平分線,設![]() 與
與![]() 交點為
交點為![]()
∵![]() ,
,
∴平行四邊形![]() 為矩形,
為矩形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∵點![]() 為
為![]() 的中點,點
的中點,點![]() 為
為![]() 的中點,
的中點,
∴![]() ,且
,且![]() ,
,
∴![]() ,
,
∴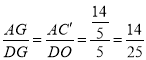 ,
,
∴![]() .
.


科目:初中數學 來源: 題型:
【題目】已知二次函數![]() (
(![]() 為常數),當自變量
為常數),當自變量![]() 的值滿足
的值滿足![]() 時,與其對應的函數值
時,與其對應的函數值![]() 的最大值為-1,則
的最大值為-1,則![]() 的值為( )
的值為( )
A. 3或6 B. 1或6 C. 1或3 D. 4或6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,漏壺是一種古代計時器.在它內部盛一定量的水,水從壺下的小孔漏出.壺內壁有刻度,人們根據壺中水面的位置計算時間.用x(小時)表示漏水時間,y(厘米)表示壺底到水面的高度,某次計時過程中,記錄到部分數據如下表:
漏水時間x(小時) | … | 3 | 4 | 5 | 6 | … |
壺底到水面高度y(厘米) | … | 9 | 7 | 5 | 3 | … |
(1)問y與x的函數關系屬于一次函數、二次函數和反比例函數中的哪一種?求出該函數解析式及自變量x的取值范圍;
(2)求剛開始計時時壺底到水面的高度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明手中有4張背面相同的撲克牌:紅桃6、紅桃9、黑桃6、黑桃9.先將4張牌背面朝上洗勻,再讓小麗抽牌.
(1)小麗從中任意抽取一張撲克牌,抽到黑桃9的概率是__________,抽到偶數的概率是_________;
(2)小麗從中任意抽取兩張撲克牌,游戲規則規定:若小麗抽到的兩張牌是一紅一黑,則小麗勝,若小麗抽到的兩張牌是一奇一偶,則小明勝,問該游戲對雙方是否公平.(利用樹狀圖或列表說明)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】面對疫情,每個人都需要積極行動起來,做好預防工作.為此某校開展了“新型冠狀病毒肺炎”防控知識競賽.現從該校五、六年級中各隨機抽取10名學生的競賽成績(百分制)進行整理、描述和分析(成績得分用![]() 表示,共分成四組:A.
表示,共分成四組:A.![]() ,B.
,B.![]() ,C.
,C.![]() ,D.
,D.![]() ),下面給出了部分信息:
),下面給出了部分信息:
五年級10名學生的競賽成績是:99,80,99,86,99,96,90,100,89,82
六年級10名學生的競賽成績在C組中的數據是:94,90,94
五、六年級抽取的學生競賽成績統計表
年級 | 平均數 | 中位數 | 眾數 | 方差 |
五年級 | 92 | 93 |
| 52 |
六年級 | 92 |
| 100 | 50.4 |
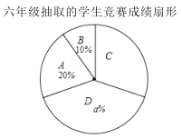
是據以上信息,解答下列問題:
(1)直接寫出上述圖表中![]() ,
,![]() ,
,![]() 的值:
的值:![]() __________,
__________,![]() ___________,
___________,![]() ___________;
___________;
(2)由以上數據,你認為該校五、六年級中哪個年級學生掌握防溺水安全知識較好?請說明理由(一條理由即可);
(3)該校五、六年級共1800人參加了此次競賽活動,估計參加此次競賽活動成績優秀![]() 的學生人數是多少?
的學生人數是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于三角函數有如下的公式:
①cos(α+β)=cosαcosβ﹣sinαsinβ;sin(α+β)=sinαcosβ+cosαsinβ;
②tan(α+β)=![]() .
.
③利用這些公式可以將一些不是特殊角的三角函數轉化為特殊角的三角函數來求值,如tan105°=tan(45°+60°)=![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.
根據上面的知識,你可以選擇適當的公式解決下面的實際問題:
(1)求cos75°的值;
(2)如圖,直升機在一建筑物CD上方的點A處測得建筑物頂端點D的俯角α為60°,底端點C的俯角β為75°,此時直升機與建筑物CD的水平距離BC為42m,求建筑物CD的高.
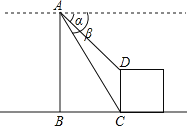
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長AB=8,E為平面內一動點,且AE=4,F為CD上一點,CF=2,連接EF,ED,則EF![]() ED的最小值為( )
ED的最小值為( )
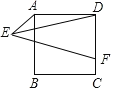
A.6![]() B.4C.4
B.4C.4![]() D.6
D.6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點,
兩點,![]() ,與直線
,與直線![]() 交于
交于![]() 、
、![]() 兩點,點
兩點,點![]() 在
在![]() 軸上,
軸上,![]() .
.
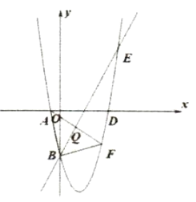
(1)求二次函數的解析式;
(2)在拋物線上有一點![]() ,若
,若![]() 的面積為
的面積為![]() ,求點
,求點![]() 的橫坐標;
的橫坐標;
(3)點![]() 在第四象限的拋物線上運動,連接
在第四象限的拋物線上運動,連接![]() ,與直線
,與直線![]() 交于點
交于點![]() ,連接
,連接![]() ,
,![]() .設
.設![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
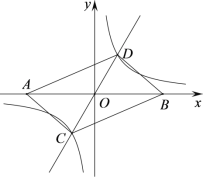
【題目】如圖,在平面直角坐標系中,點A的坐標為(m,0),m<0,點B與點A 關于原點對稱,直線![]() 與雙曲線
與雙曲線![]() 交于C,D兩點.
交于C,D兩點.
(1)直接判斷后填空:四邊形ACBD的形狀一定是 ;
(2)若點D(1,t),求雙曲線的解析式;
(3)在(2)的前提下,四邊形ACBD為矩形時,求m的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com