
【題目】如圖,AB是⊙O的切線,B為切點,AC經過點O,與⊙O分別相交于點D,C.若∠ACB=30°,AB= ![]() ,則陰影部分的面積是( )
,則陰影部分的面積是( ) 
A.![]()
B.![]()
C.![]() ﹣
﹣ ![]()
![]()
D.![]() ﹣
﹣ ![]()
![]()
【答案】C
【解析】解:連接OB.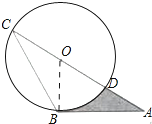
∵AB是⊙O切線,
∴OB⊥AB,
∵OC=OB,∠C=30°,
∴∠C=∠OBC=30°,
∴∠AOB=∠C+∠OBC=60°,
在RT△ABO中,∵∠ABO=90°,AB= ![]() ,∠A=30°,
,∠A=30°,
∴OB=1,
∴S陰=S△ABO﹣S扇形OBD= ![]() ×1×
×1× ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() .
.
故選C.
【考點精析】本題主要考查了切線的性質定理和扇形面積計算公式的相關知識點,需要掌握切線的性質:1、經過切點垂直于這條半徑的直線是圓的切線2、經過切點垂直于切線的直線必經過圓心3、圓的切線垂直于經過切點的半徑;在圓上,由兩條半徑和一段弧圍成的圖形叫做扇形;扇形面積S=π(R2-r2)才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】已知拋物線C:y=x2﹣3x+m,直線l:y=kx(k>0),當k=1時,拋物線C與直線l只有一個公共點.
(1)求m的值;
(2)若直線l與拋物線C交于不同的兩點A,B,直線l與直線l1:y=﹣3x+b交于點P,且 ![]() +
+ ![]() =
= ![]() ,求b的值;
,求b的值;
(3)在(2)的條件下,設直線l1與y軸交于點Q,問:是否在實數k使S△APQ=S△BPQ?若存在,求k的值,若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形OABC中,OA=3,OC=2,F是AB上的一個動點(F不與A,B重合),過點F的反比例函數y= ![]() (k>0)的圖象與BC邊交于點E.
(k>0)的圖象與BC邊交于點E.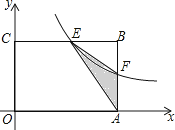
(1)當F為AB的中點時,求該函數的解析式;
(2)當k為何值時,△EFA的面積最大,最大面積是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線y=﹣2x+10與x軸,y軸相交于A,B兩點,點C的坐標是(8,4),連接AC,BC.
(1)求過O,A,C三點的拋物線的解析式,并判斷△ABC的形狀;
(2)動點P從點O出發,沿OB以每秒2個單位長度的速度向點B運動;同時,動點Q從點B出發,沿BC以每秒1個單位長度的速度向點C運動.規定其中一個動點到達端點時,另一個動點也隨之停止運動.設運動時間為t秒,當t為何值時,PA=QA?
(3)在拋物線的對稱軸上,是否存在點M,使以A,B,M為頂點的三角形是等腰三角形?若存在,求出點M的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解市民對全市創衛工作的滿意程度,某中學教學興趣小組在全市甲、乙兩個區內進行了調查統計,將調查結果分為不滿意,一般,滿意,非常滿意四類,回收、整理好全部問卷后,得到下列不完整的統計圖.
請結合圖中信息,解決下列問題:
(1)求此次調查中接受調查的人數.
(2)求此次調查中結果為非常滿意的人數.
(3)興趣小組準備從調查結果為不滿意的4位市民中隨機選擇2為進行回訪,已知4為市民中有2位來自甲區,另2位來自乙區,請用列表或用畫樹狀圖的方法求出選擇的市民均來自甲區的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com