【題目】一次函數y=kx+b（k≠0）的圖象經過點A（2，﹣6），且與反比例函數y=﹣ 
的圖象交于點B（a，4）
（1）求一次函數的解析式；
（2）將直線AB向上平移10個單位后得到直線l：y1=k1x+b1（k1≠0），l與反比例函數y2= 
的圖象相交，求使y1＜y2成立的x的取值范圍．
【答案】
（1）解：∵反比例函數y=﹣ 
的圖象過點B（a，4），
∴4=﹣ 
，解得：a=﹣3，
∴點B的坐標為（﹣3，4）．
將A（2，﹣6）、B（﹣3，4）代入y=kx+b中，
，解得： 
，
∴一次函數的解析式為y=﹣2x﹣2．
（2）解：直線AB向上平移10個單位后得到直線l的解析式為：y1=﹣2x+8．
聯立直線l和反比例函數解析式成方程組，
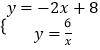，解得： 
， 
，
∴直線l與反比例函數圖象的交點坐標為（1，6）和（3，2）．
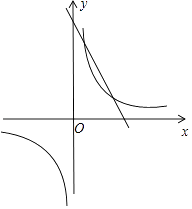
畫出函數圖象，如圖所示．
觀察函數圖象可知：當0＜x＜1或x＞3時，反比例函數圖象在直線l的上方，
∴使y1＜y2成立的x的取值范圍為0＜x＜1或x＞3．
【解析】（1）根據點B的縱坐標利用反比例函數圖象上點的坐標特征可求出點B的坐標，根據點A、B的坐標利用待定系數法即可求出直線AB的解析式；（2）根據“上加下減”找出直線l的解析式，聯立直線l和反比例函數解析式成方程組，解方程組可找出交點坐標，畫出函數圖象，根據兩函數圖象的上下位置關系即可找出使y1＜y2成立的x的取值范圍．
黃岡創優卷系列答案科目：初中數學 來源： 題型：
【題目】如圖，已知直線l與⊙O相離，OA⊥l于點A，交⊙O于點P，點B是⊙O上一點，連接BP并延長，交直線l于點C，使得AB=AC．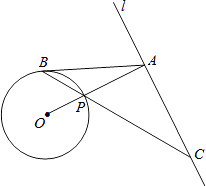 
（1）求證：AB是⊙O的切線；
（2）PC=2 
，OA=4． ①求⊙O的半徑；
②求線段PB的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，在銳角△ABC中，∠ABC=45°，高線AD、BE相交于點F．
（1）判斷BF與AC的數量關系并說明理由；
（2）如圖2，將△ACD沿線段AD對折，點C落在BD上的點M，AM與BE相交于點N，當DE∥AM時，判斷NE與AC的數量關系并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知拋物線y= 
x2+1具有如下性質：該拋物線上任意一點到定點F（0，2）的距離與到x軸的距離始終相等，如圖，點M的坐標為（ 
，3），P是拋物線y= x2+1上一個動點，則△PMF周長的最小值是（ ）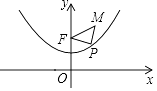 
A.3
B.4
C.5
D.6
查看答案和解析>>
科目：初中數學 來源： 題型：
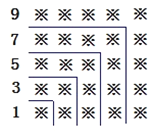
【題目】“數形結合"是一種重要的數學思想，觀察下面的圖形和算式.
解答下列問題：
(1)試猜想1+3+5+7+9+…+19=______=（ ）；
(2)試猜想，當n是正整數時，1+3+5+7+9+…+(2n-1)= ；
(3)請用（2）中得到的規律計算：19+21+23+25+27+…+99.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為響應珠海環保城市建設，我市某污水處理公司不斷改進污水處理設備，新設備每小時處理污水量是原系統的1.5倍，原來處理1200m3污水所用的時間比現在多用10小時．
（1）原來每小時處理污水量是多少m2？
（2）若用新設備處理污水960m3，需要多長時間？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】綜合題。
（1）如圖1，已知AD=BC，AC=BD．求證：△ADB≌△BCA．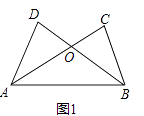 
（2）如圖2，已知AB是⊙O的一條直徑，延長AB至點C，使AC=3BC，CD與⊙O相切于點D，若CD= 
，求⊙O的半徑．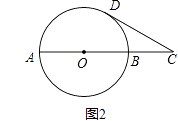 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
