
【題目】我們規(guī)定,以二次函數(shù)![]() 的二次項(xiàng)系數(shù)
的二次項(xiàng)系數(shù)![]() 的2倍為一次項(xiàng)系數(shù),一次項(xiàng)系數(shù)
的2倍為一次項(xiàng)系數(shù),一次項(xiàng)系數(shù)![]() 為常數(shù)項(xiàng)構(gòu)造的一次函數(shù)
為常數(shù)項(xiàng)構(gòu)造的一次函數(shù)![]() 叫做二次函數(shù)
叫做二次函數(shù)![]() 的“子函數(shù)”,反過來,二次函數(shù)
的“子函數(shù)”,反過來,二次函數(shù)![]() 叫做一次函數(shù)
叫做一次函數(shù)![]() 的“母函數(shù)”.
的“母函數(shù)”.
(1)若一次函數(shù)![]() 是二次函數(shù)
是二次函數(shù)![]() 的“子函數(shù)”,且二次函數(shù)經(jīng)過點(diǎn)
的“子函數(shù)”,且二次函數(shù)經(jīng)過點(diǎn)![]() ,求此二次函數(shù)的解析式.
,求此二次函數(shù)的解析式.
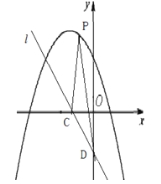
(2)如圖,已知二次函數(shù)![]() 的“子函數(shù)”圖象直線
的“子函數(shù)”圖象直線![]() 與
與![]() 軸、
軸、![]() 軸交于
軸交于![]() 、
、![]() 兩點(diǎn),點(diǎn)
兩點(diǎn),點(diǎn)![]() 是直線
是直線![]() 上方的拋物線上任意一點(diǎn),求
上方的拋物線上任意一點(diǎn),求![]() 的面積的最大值.
的面積的最大值.
(3)已知二次函數(shù)![]() 與它的“子函數(shù)”
與它的“子函數(shù)”![]() 的函數(shù)圖象有兩個(gè)交點(diǎn)
的函數(shù)圖象有兩個(gè)交點(diǎn)![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
【答案】(1)![]() ;(2)13;(3)
;(2)13;(3)![]() ,-6,6
,-6,6
【解析】
(1)由題意得:![]() ,
,![]() ,故拋物線的表達(dá)式為:
,故拋物線的表達(dá)式為:![]() ,將點(diǎn)C的坐標(biāo)代入即可求解;
,將點(diǎn)C的坐標(biāo)代入即可求解;
(2)連接DP,過點(diǎn)P作y軸的平行線交CD于點(diǎn)H,設(shè)點(diǎn)P(![]() ,
,![]() ),則點(diǎn)H(
),則點(diǎn)H(![]() ,
,![]() ),由S△PCD=S△PHC-S△PHD=
),由S△PCD=S△PHC-S△PHD=![]() 構(gòu)造關(guān)于m的二次函數(shù),利用二次函數(shù)的性質(zhì)即可求解;
構(gòu)造關(guān)于m的二次函數(shù),利用二次函數(shù)的性質(zhì)即可求解;
(3)由二次函數(shù)![]() 的“子函數(shù)”為
的“子函數(shù)”為![]() ,知
,知![]() ,
,![]() ,聯(lián)立
,聯(lián)立![]() 與
與![]() 得
得![]() ,利用根與系數(shù)的關(guān)系結(jié)合已知條件
,利用根與系數(shù)的關(guān)系結(jié)合已知條件![]() 即可求解.
即可求解.
(1)由題意得:![]() ,
,![]() ,
,
故拋物線的表達(dá)式為:![]() ,將點(diǎn)C(3,0)的坐標(biāo)代入得:
,將點(diǎn)C(3,0)的坐標(biāo)代入得:![]() ,
,
解得:c=3,
故拋物線的表達(dá)式為:![]() ;
;
(2)如圖所示,連接DP,

設(shè)點(diǎn)P(![]() ,
,![]() ),
),
二次函數(shù)![]() 中,
中,![]() ,
,![]() ,
,
∴“子函數(shù)”圖象直線![]() 的表達(dá)式為:
的表達(dá)式為:![]() ,
,
令![]() ,則
,則![]() ;令
;令![]() ,則
,則![]() ;
;
∴點(diǎn)C、D的坐標(biāo)分別為(-2,0)、(0,-4),
過點(diǎn)P作y軸的平行線交CD于點(diǎn)H,則點(diǎn)H(![]() ,
,![]() ),
),
∴S△PCD=S△PHC-S△PHD=![]()
![]()
![]()
![]() ,
,
∵![]() ,∴S△PCD有最大值,
,∴S△PCD有最大值,
當(dāng)![]() 時(shí),其最大值為13;
時(shí),其最大值為13;
(3)由二次函數(shù)![]() 的“子函數(shù)”為
的“子函數(shù)”為![]() ,
,
知:![]() ,
,![]() ,
,
∴二次函數(shù)的解析式為![]() ,其“子函數(shù)”為
,其“子函數(shù)”為![]() ,
,
聯(lián)立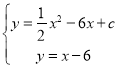 ,
,
消去![]() 得
得![]() ,
,
由根與系數(shù)的關(guān)系得:![]() ,
,![]() ,
,
∵![]() ,
,
整理得:![]() ,
,
∴![]() ,
,
解得:![]() .
.
故![]() 的值分別為:
的值分別為:![]() ,
,![]() ,
,![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
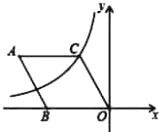
【題目】如圖,在菱形ABOC中,AB=2,∠A=60°,菱形的一個(gè)頂點(diǎn)C在反比例函數(shù)y=![]() (k≠0)的圖象上,則反比例函數(shù)的解析式為( )
(k≠0)的圖象上,則反比例函數(shù)的解析式為( )
A.y=![]() B.y=
B.y=![]() C.y=
C.y=![]() D.y=
D.y=![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】2020年3月至5月,某校開展了一系列居家閱讀活動(dòng).學(xué)生利用“宅家”時(shí)光,在書海中遨游,從閱讀中獲得精神慰藉和自我提升.為了解學(xué)生居家閱讀的情況,學(xué)校從七、八兩個(gè)年級各隨機(jī)抽取50名學(xué)生,進(jìn)行了居家閱讀情況調(diào)查.下面給出了部分?jǐn)?shù)據(jù)信息:
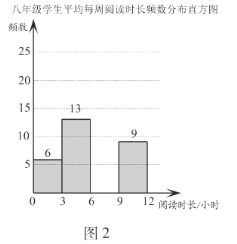
![]() .兩個(gè)年級學(xué)生平均每周閱讀時(shí)長
.兩個(gè)年級學(xué)生平均每周閱讀時(shí)長![]() (單位:小時(shí))的頻數(shù)分布直方圖如下(數(shù)據(jù)分成4組:
(單位:小時(shí))的頻數(shù)分布直方圖如下(數(shù)據(jù)分成4組:![]() ,
,![]() ,
,![]() ,
,![]() ):
):

b.七年級學(xué)生平均每周閱讀時(shí)長在![]() 這一組的是:6 6 7 7 7 7 7 8 8 8 8 8 8 8 8 8
這一組的是:6 6 7 7 7 7 7 8 8 8 8 8 8 8 8 8
c.兩個(gè)年級學(xué)生平均每周閱讀時(shí)長的平均數(shù)、中位數(shù)、眾數(shù)、方差如下:
平均數(shù) | 中位數(shù) | 眾數(shù) | 方差 | |
七年級 | 6.3 |
| 8 | 7.0 |
八年級 | 6.0 | 7 | 7 | 6.3 |
根據(jù)以上信息,回答下列問題:
(1)補(bǔ)全圖2;
(2)寫出表中![]() 的值;
的值;
(3)返校后,學(xué)校計(jì)劃將平均每周閱讀時(shí)長不低于9小時(shí)的學(xué)生授予“閱讀之星”稱號.小麗說:“根據(jù)頻數(shù)分布直方圖中的數(shù)據(jù)信息,估計(jì)七年級約有20%的學(xué)生獲得該稱號,八年級約有18%的學(xué)生獲得該稱號,所以七年級獲得該稱號的人數(shù)一定比八年級獲得該稱號的人數(shù)多.”你認(rèn)為她的說法________(填入“正確”或“錯(cuò)誤”);
(4)請你結(jié)合數(shù)據(jù)對兩個(gè)年級的居家閱讀情況進(jìn)行評價(jià).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
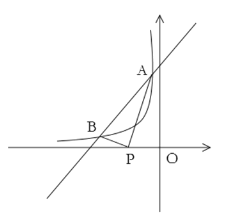
【題目】如圖,一次函數(shù)![]() 與反比例函數(shù)
與反比例函數(shù)![]() 的圖象交于點(diǎn)A(a,3)和B(-3,1).
的圖象交于點(diǎn)A(a,3)和B(-3,1).
(1)求k、b的值.
(2)點(diǎn)P是x軸上一點(diǎn),連接PA,PB,當(dāng)△PAB的周長最小時(shí)求點(diǎn)P的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,正方形![]() .... 按如圖的方式放置.點(diǎn)
.... 按如圖的方式放置.點(diǎn)![]()
![]() 和點(diǎn)
和點(diǎn)![]() 分別落在直線
分別落在直線![]() 和
和![]() 軸上.拋物線
軸上.拋物線![]() 過點(diǎn)
過點(diǎn)![]() ,且頂點(diǎn)在直線
,且頂點(diǎn)在直線![]() 上,拋物線
上,拋物線![]() 過點(diǎn)
過點(diǎn)![]() ,且頂點(diǎn)在直線
,且頂點(diǎn)在直線![]() 上,...按此規(guī)律,拋物線
上,...按此規(guī)律,拋物線![]() ,過點(diǎn)
,過點(diǎn)![]() , 且頂點(diǎn)也在直線
, 且頂點(diǎn)也在直線![]() 上,其中拋物線
上,其中拋物線![]() 交正方形
交正方形![]() 的邊
的邊![]() 于點(diǎn)
于點(diǎn)![]() ,拋物線
,拋物線![]() 交正方形
交正方形![]() 的邊
的邊![]() 于點(diǎn)
于點(diǎn)![]() (其中
(其中![]() 且
且![]() 為正整數(shù)) .
為正整數(shù)) .

(1)直接寫出下列點(diǎn)的坐標(biāo):![]() ,
,![]() ;
;
(2)寫出拋物線![]() 的解析式,并寫出拋物線
的解析式,并寫出拋物線![]() 的解析式求解過程,再猜想拋物線
的解析式求解過程,再猜想拋物線![]() 的頂點(diǎn)坐標(biāo);
的頂點(diǎn)坐標(biāo);
(3)設(shè)![]() ,試判斷
,試判斷![]() 與
與![]() 的數(shù)量關(guān)系并說明理由.
的數(shù)量關(guān)系并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某租賃公司有![]() 型兩種客車,它們的載客量和租金標(biāo)準(zhǔn)如下:
型兩種客車,它們的載客量和租金標(biāo)準(zhǔn)如下:
客車類型 | 載客量(人/輛) | 租金(元/輛) |
| 45 | 400 |
| 30 | 280 |
如果某學(xué)校計(jì)劃組織195名師生到培訓(xùn)基地參加社會(huì)實(shí)踐活動(dòng),那么租車的總費(fèi)用最低為____________________元.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在菱形ABCD中,AB=6,∠DAB=60°,AE分別交BC、BD于點(diǎn)E、F,若CE=2,連接CF.以下結(jié)論:①∠BAF=∠BCF; ②點(diǎn)E到AB的距離是2![]() ; ③S△CDF:S△BEF=9:4; ④tan∠DCF=3/7. 其中正確的有()
; ③S△CDF:S△BEF=9:4; ④tan∠DCF=3/7. 其中正確的有()
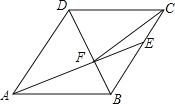
A. 4個(gè) B. 3個(gè) C. 2個(gè) D. 1個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
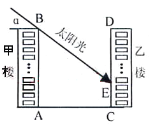
【題目】下圖為某小區(qū)的兩幢1O層住宅樓,由地面向上依次為第1層、第2層、…、第10層,每層的高度為3m,兩樓間的距離AC=30m.現(xiàn)需了解在某一時(shí)段內(nèi),甲樓對乙樓的采光的影響情況.假設(shè)某一時(shí)刻甲樓樓頂B落在乙樓的影子長EC=h,太陽光線與水平線的夾角為α.
(1)用含α的式子表示h;
(2)當(dāng)α=30°時(shí),甲樓樓頂B的影子落在乙樓的第幾層?從此時(shí)算起,若α每小時(shí)增加10°,幾小時(shí)后,甲樓的影子剛好不影響乙樓采光.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com