【題目】在平面直角坐標系xOy中，拋物線y＝ax2﹣4ax+3a的最高點的縱坐標是2．
（1）求拋物線的對稱軸及拋物線的表達式；
（2）將拋物線在1≤x≤4之間的部分記為圖象G1，將圖象G1沿直線x＝1翻折，翻折后的圖象記為G2，圖象G1和G2組成圖象G．過（0，b）作與y軸垂直的直線l，當直線l和圖象G只有兩個公共點時，將這兩個公共點分別記為P1（x1，y1），P（x2，y2），求b的取值范圍和x1+x2的值．
【答案】（1）y＝﹣2x2+8x﹣6；（2）b＝2或﹣6≤b＜0，x1+x2＝2．
【解析】
（1）依據配方法將函數關系式變形為y＝a（x﹣2）2﹣a，再依據頂點縱坐標為2可求得a的值，從而可求得拋物線的解析式；
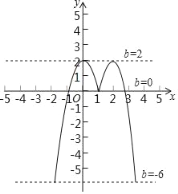
（2）先根據題意畫出圖形，由圖象可知b＝2或﹣6≤b＜0，由圖象的對稱性可求x1+x2的值．
（1）∵拋物線y＝ax2﹣4ax+3a＝a（x﹣2）2﹣a，
∴對稱軸為直線x＝2，
∵拋物線y＝ax2﹣4ax+3a的最高點的縱坐標是2，
∴a＝﹣2，
∴拋物線的表達式為y＝﹣2（x﹣2）2+2＝﹣2x2+8x﹣6；
（2）如圖，由圖象可知b＝2或﹣6≤b＜0，
由圖象的對稱性可得：x1+x2＝2．
科目：初中數學 來源： 題型：
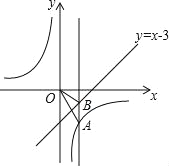
【題目】如圖，已知點A在反比函數y＝
（k＜0）的圖象上，點B在直線y＝x﹣3的圖象上，點B的縱坐標為﹣1，AB⊥x軸，且S△OAB＝4．
（1）求點A的坐標和k的值；
（2）若點P在反比例函數y＝（k＜0）的圖象上，點Q在直線y＝x﹣3的圖象上，P、Q兩點關于y軸對稱，設點P的坐標為（m，n），求
+
的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某品牌牛奶供應商提供A，B，C，D四種不同口味的牛奶供學生飲用．某校為了了解學生對不同口味的牛奶的喜好，對全校訂牛奶的學生進行了隨機調查，并根據調查結果繪制了如下兩幅不完整的統計圖．根據統計圖的信息解決下列問題：
（1）本次調查的學生有多少人？
（2）補全上面的條形統計圖；
（3）扇形統計圖中C對應的中心角度數是_____；
（4）若該校有600名學生訂了該品牌的牛奶，每名學生每天只訂一盒牛奶，要使學生能喝到自己喜歡的牛奶，則該牛奶供應商送往該校的牛奶中，A，B口味的牛奶共約多少盒？
查看答案和解析>>
科目：初中數學 來源： 題型：
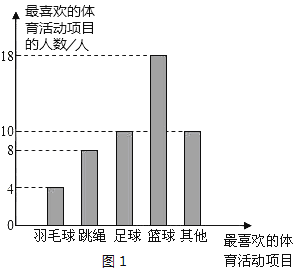
【題目】某校圍繞著“你最喜歡的體育活動項目是什么？（只寫一項）”的問題，對在校學生進行了隨機抽樣調查，從而得到一組數據，如圖1是根據這組數據繪制的條形統計圖，請結合統計圖回答下列問題：
（1）該校對多少名學生進行了抽樣調查？
（2）本次抽樣調查中，最喜歡足球活動的有多少人？占被調查人數的百分比是多少？
（3）若該校九年級共有400名學生，圖2是根據各年級學生人數占全校學生總人數的百分比繪制的扇形統計圖，請你估計全校學生中最喜歡籃球活動的人數約為多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
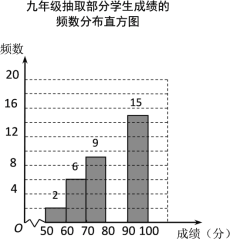
【題目】某校組織九年級學生參加漢字聽寫大賽，并隨機抽取部分學生成績作為樣本進行分析，繪制成如下的統計表：
成績x/分 | 頻數 | 頻率 | |
第1段 | x＜60 | 2 | 0.04 |
第2段 | 60≤x＜70 | 6 | 0.12 |
第3段 | 70≤x＜80 | 9 | b |
第4段 | 80≤x＜90 | a | 0.36 |
第5段 | 90≤x≤100 | 15 | 0.30 |
請根據所給信息，解答下列問題：
（1）a＝______，b＝______；
（2）請補全頻數分布直方圖；
（3）樣本中，部分學生成績的中位數落在第_______段；
（4）已知該年級有400名學生參加這次比賽，若成績在90分以上（含90分）的為優，估計該年級成績為優的有多少人？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】圖中是小明完成的一道作業題，請你參考小明答方法解答下面的問題：
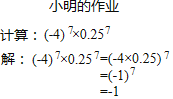
（1）計算：①82008×（﹣0.125）2008；
②（
）11×（﹣
）13×（
）12．
（2）若24n16n＝219，求n的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖是拋物線y1=ax2+bx+c（a≠0）圖象的一部分，拋物線的頂點坐標A（1，3），與x軸的一個交點B（4，0），直線y2=mx+n（m≠0）與拋物線交于A，B兩點，下列結論：
①2a+b=0；②abc＞0；③方程ax2+bx+c=3有兩個相等的實數根；④拋物線與x軸的另一個交點是（﹣1，0）；⑤當1＜x＜4時，有y2＜y1，
其中正確的是（ ）
A. ①②③ B. ①③④ C. ①③⑤ D. ②④⑤
查看答案和解析>>
科目：初中數學 來源： 題型：
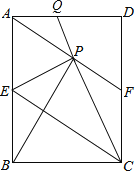
【題目】如圖，在矩形ABCD中，E是AB邊的中點，沿EC對折矩形ABCD，使B點落在點P處，折痕為EC，連結AP并延長AP交CD于F點，連結CP并延長CP交AD于Q點．給出以下結論：
①四邊形AECF為平行四邊形；
②∠PBA=∠APQ；
③△FPC為等腰三角形；
④△APB≌△EPC．
其中正確結論的個數為（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】劉帥參加“我學十九大”知識競賽，再答對最后兩道單選題就能問鼎冠軍．第一道單選題有3個選項，第二道單選題有4個選項，這兩道題劉帥都不會，不過劉帥還有一個“求助”沒有用（使用“求助”可以讓主持人去掉其中一題的一個錯誤選項）．
（1）如果劉帥第一題不使用“求助”，那么劉帥答對第一道題的概率是 ．
（2）從概率的角度分析，你建議劉帥在第幾題使用“求助”，說明你的理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com