
【題目】已知點C是線段AB的中點,點D是線段BC上一點,下列條件不能確定點D是線段BC的中點的是( )
A.CD=DBB.BD=![]() ADC.2AD=3BCD.3AD=4BC
ADC.2AD=3BCD.3AD=4BC
科目:初中數學 來源: 題型:
【題目】如圖,邊長為4個單位長度的正方形ABCD的邊AB與等腰直角三角形EFG的斜邊FG重合,△EFG
以每秒1個單位長度的速度沿BC向右勻速運動(保持FG⊥BC),當點E運動到CD邊上時△EFG停止
運動.設△EFG的運動時間為t秒,△EFG與正方形ABCD重疊部分的面積為S,則S關于t的函數大
致圖象為( )
A. 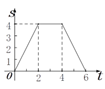 B.
B. 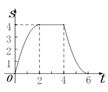 C.
C. 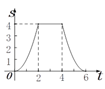 D.
D. 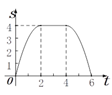
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,AB=AC,BC交⊙O于點D, AC交⊙O于點E,∠BAC=45°。
(1)求∠EBC的度數;
(2)求證:BD=CD。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,過點D 作![]() 于點E,點F在邊CD上,DF=BE,連接AF,BF.
于點E,點F在邊CD上,DF=BE,連接AF,BF.

(1)求證:四邊形EBFD是矩形;
(2)若AE=3,DE=4,DF=5,求證:AF平分![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】規定:如果關于x的一元二次方程ax2+bx+c=0(a≠0)有兩個實數根,且其中一個根是另一個根的2倍,則稱這樣的方程為“倍根方程”.現有下列結論: ①方程x2+2x﹣8=0是倍根方程;
②若關于x的方程x2+ax+2=0是倍根方程,則a=±3;
③若關于x的方程ax2﹣6ax+c=0(a≠0)是倍根方程,則拋物線y=ax2﹣6ax+c與x軸的公共點的坐標是(2,0)和(4,0);
④若點(m,n)在反比例函數y=![]() 的圖象上,則關于x的方程mx2+5x+n=0是倍根方程.
的圖象上,則關于x的方程mx2+5x+n=0是倍根方程.
上述結論中正確的有( )
A. ①② B. ③④ C. ②③ D. ②④
查看答案和解析>>
科目:初中數學 來源: 題型:
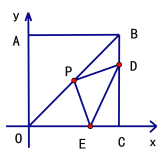
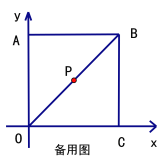
【題目】在直角坐標系中,正方形OABC的邊長為8,連結OB,P為OB的中點.
(1)直接寫出點B的坐標B( , )
(2)點D從B點出發,以每秒1個單位長度的速度在線段BC上向終點C運動,連結PD,作PD⊥PE,交OC于點E,連結DE.設點D的運動時間為![]() 秒.
秒.
①點D在運動過程中,∠PED的大小是否發生變化?如果變化,請說明理由如果不變,求出∠PED的度數
②連結PC,當PC將△PDE分成的兩部分面積之比為1:2時,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1所示∠AOB的紙片,OC平分∠AOB,如圖2把∠AOB沿OC對折成∠COB(OA與OB重合),從O點引一條射線OE,使∠BOE=![]() ∠EOC,再沿OE把角剪開,若剪開后得到的3個角中最大的一個角為76°,則∠AOB=_____________°.
∠EOC,再沿OE把角剪開,若剪開后得到的3個角中最大的一個角為76°,則∠AOB=_____________°.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠有甲種原料130kg,乙種原料144kg.現用這兩種原料生產出A,B兩種產品共30件.已知生產每件A產品需甲種原料5kg,乙種原料4kg,且每件A產品可獲利700元;生產每件B產品需甲種原料3kg,乙種原料6kg,且每件B產品可獲利900元.設生產A產品x件(產品件數為整數件),根據以上信息解答下列問題:
(1)生產A,B兩種產品的方案有哪幾種;
(2)設生產這30件產品可獲利y元,寫出y關于x的函數解析式,寫出(1)中利潤最大的方案,并求出最大利潤.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com