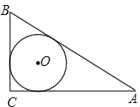
【題目】如圖，△ABC中，若AC=4，BC=3，AB=5，則△ABC的內切圓半徑R=_____．
英才計劃同步課時高效訓練系列答案科目：初中數學 來源： 題型：
【題目】如圖，I是ABC的內心，AI向延長線和△ABC的外接圓相交于點D，連接BI，BD，DC下列說法中錯誤的一項是（ ）
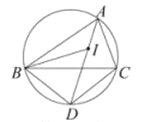
A．線段DB繞點D順時針旋轉一定能與線段DC重合
B．線段DB繞點D順時針旋轉一定能與線段DI熏合
C．∠CAD繞點A順時針旋轉一定能與∠DAB重合
D．線段ID繞點I順時針旋轉一定能與線段IB重合
查看答案和解析>>
科目：初中數學 來源： 題型：
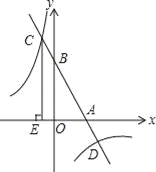
【題目】已知點P在一次函數y=kx+b（k，b為常數，且k＜0，b＞0）的圖象上，將點P向左平移1個單位，再向上平移2個單位得到點Q，點Q也在該函數y=kx+b的圖象上．
（1）k的值是 ；
（2）如圖，該一次函數的圖象分別與x軸、y軸交于A，B兩點，且與反比例函數y=
圖象交于C，D兩點（點C在第二象限內），過點C作CE⊥x軸于點E，記S1為四邊形CEOB的面積，S2為△OAB的面積，若
=
，則b的值是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
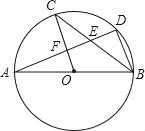
【題目】如圖，AB是⊙O的直徑，C，D是⊙O上的點，且OC∥BD，AD分別與BC，OC相交于點E，F，則下列結論：①AD⊥BD；②∠AOC=∠AEC；③CB平分∠ABD；④AF=DF；⑤BD=2OF；⑥△CEF≌△BED，其中一定成立的____（把你認為正確結論的序號都填上）
查看答案和解析>>
科目：初中數學 來源： 題型：
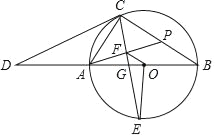
【題目】如圖，AB為⊙O的直徑，CD切⊙O于點C，與BA的延長線交于點D，OE⊥AB交⊙O于點E，連接CA、CE、CB，CE交AB于點G，過點A作AF⊥CE于點F，延長AF交BC于點P．
（Ⅰ）求∠CPA的度數；
（Ⅱ）連接OF，若AC=
，∠D=30°，求線段OF的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
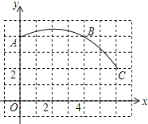
【題目】如圖，一段圓弧與長度為1的正方形網格的交點是A、B、C．
(1)請完成以下操作：
①以點O為原點，垂直和水平方向為軸，網格邊長為單位長，建立平面直角坐標系；
②根據圖形提供的信息，標出該圓弧所在圓的圓心D，并連接AD、CD；
(2)請在(1)的基礎上，完成下列填空：⊙D的半徑為__________；點（6，–2）在⊙D__________；（填“上”、“內”、“外”）∠ADC的度數為__________．
查看答案和解析>>
科目：初中數學 來源： 題型：
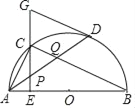
【題目】如圖，AB是半圓O的直徑，點D是半圓O上一點，點C是
的中點，CE⊥AB于點E，過點D的切線交EC的延長線于點G，連接AD，分別交CE、CB于點P、Q，連接AC．
（1）求證：GP＝GD；
（2）求證：P是線段AQ的中點；
（3）連接CD，若CD＝2，BC＝4，求⊙O的半徑和CE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
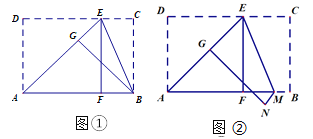
【題目】李剛和常明兩人在數學活動課上進行折紙創編活動.李剛拿起一張準備好的長方形紙片對常明說:“我現在折疊紙片（圖①），使點D落在AB邊的點F處，得折痕AE，再折疊，使點C落在AE邊的點G處，此時折痕恰好經過點B，如果AD=
，那么AB長是多少？”常明說；“簡單，我會. AB應該是_____”.
常明回答完，又對李剛說：“你看我的創編（圖②），與你一樣折疊，可是第二次折疊時，折痕不經過點B，而是經過了AB邊上的M點，如果AD=，測得EC=3BM，那么AB長是多少？”李剛思考了一會，有點為難，聰明的你，你能幫忙解答嗎？AB=_____.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，建筑物AB的高為6cm，在其正東方向有個通信塔CD，在它們之間的地面點M（B，M，D三點在一條直線上）處測得建筑物頂端A、塔項C的仰角分別為37°和60°，在A處測得塔頂C的仰角為30°，則通信塔CD的高度．（sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，
=1.73，精確到0.1m）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
