
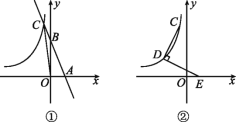
【題目】如圖①,直線y=-2x+4交x軸、y軸于A,B兩點,交雙曲線y=![]() (x<0)于C點,△OAC的面積為6.
(x<0)于C點,△OAC的面積為6.
(1)求雙曲線的解析式;
(2)如圖②,D為雙曲線y=![]() (x<0)上一點,連接CD,將線段CD繞點D順時針旋轉90°得線段DE,點E恰好落在x軸上,求點E的坐標.
(x<0)上一點,連接CD,將線段CD繞點D順時針旋轉90°得線段DE,點E恰好落在x軸上,求點E的坐標.
【答案】(1)y=-![]() ;(2)點E的坐標為(1,0)
;(2)點E的坐標為(1,0)
【解析】
(1)過C作CH⊥x軸于H,根據△AOC的面積為6,求得CH=6,即可得出C(-1,6),代入y=![]() (x<0)可得,k=-6;
(x<0)可得,k=-6;
(2)過點D作DF⊥x軸于F,過C作CG⊥DF于G,則∠G=∠DFE=90°,再根據旋轉的性質,判定△DCG≌△EDF(AAS),即可得出CG=DF,DG=EF,再設D(m,-![]() ),則DF=-
),則DF=-![]() ,FO=-a,根據C(-1,6),可得CG=-1-m,DF=-1-m,進而得出方程-
,FO=-a,根據C(-1,6),可得CG=-1-m,DF=-1-m,進而得出方程-![]() =-1-m,解得m=-3或m=2(舍去),最后根據OE=4-3=1,可得E(1,0).
=-1-m,解得m=-3或m=2(舍去),最后根據OE=4-3=1,可得E(1,0).
解:(1)由題意得A(2,0),B(0,4),OA=2,
∵S△OAC=![]() ·OA·yc=6,∴yc=6.
·OA·yc=6,∴yc=6.
∵點C在直線y=-2x+4上,
∴6=-2x+4,∴x=-1,∴點C的坐標為(-1,6).
∵點C在雙曲線y=![]() (x<0)上,∴6=
(x<0)上,∴6=![]() ,解得k=-6.
,解得k=-6.
∴雙曲線的解析式為y=-![]() .
.
(2)過點D作DF⊥x軸于F,過C作CG⊥DF于G,則∠G=∠DFE=90°,
由旋轉可得,CD=DE,∠CDE=90°,

∴∠CDG=∠DEF,
在△DCG和△EDF中,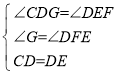 ,
,
∴△DCG≌△EDF(AAS),
∴CG=DF,DG=EF,
設D的坐標為![]() m,-
m,-![]()
![]() ,則DF=-
,則DF=-![]() ,FO=-m,
,FO=-m,
∵C(-1,6),
∴CG=-1-a,
∴DF=-1-a,
∴-![]() =-1-a,
=-1-a,
解得a=-3或a=2(舍去),
∴DF=-1+3=2,DG=GF-DF=6-2=4,
∴EF=4,
又∵FO=3,
∴OE=4-3=1,
∴點E的坐標為(1,0).


 開心練習課課練與單元檢測系列答案
開心練習課課練與單元檢測系列答案科目:初中數學 來源: 題型:
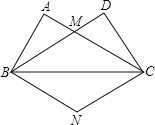
【題目】如圖,在△ABC和△DCB中,AB=DC,∠A=∠D,AC、DB交于點M.
(1)求證:△ABC≌△DCB;
(2)作CN∥BD,BN∥AC,CN交BN于點N,四邊形BNCM是什么四邊形?請證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校準備在各班設立圖書角以豐富同學們的課余文化生活.為了更合理的搭配各類書籍,學校團委以“我最喜愛的書籍”為主題,對學生最喜愛的一種書籍類型進行隨機抽樣調查,收集整理數據后,繪制出以下兩幅未完成的統計圖,請根據圖①和圖②提供的信息,解答下列問題:
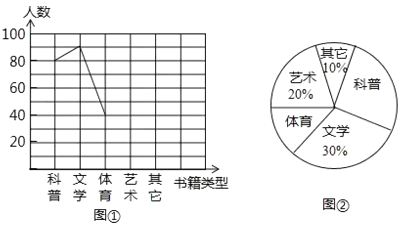
(1)在這次抽樣調查中,一共調查了_____________名學生;
(2)請把折線統計圖補充完整;
(3)在統計圖②中,求出“體育”部分所對應的圓心角的度數;
(4)若該校有學生2400人,估計喜歡“科普”書籍的有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了了解學生使用手機情況,隨機抽取了部分學生進行|使用手機的目的和每周使用手機的時間的問卷調查,并繪制成如圖所示的統計圖,已知“查資料”的人數為38人。
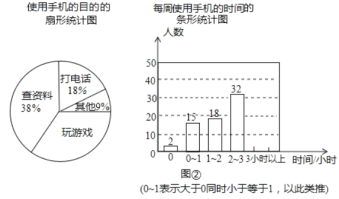
根據以上信息,回答下列問題:
(1)這次調查中,一共抽查了__________名學生;
(2)在扇形統計圖中,“玩游戲”所對應的圓心角的度數是___________度;
(3)補全條形統計圖;
(4)若該校共有學生2000人,請你估計每周使用手機時間超過2小時的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是 ( )
A.要調查現在人們在數學化時代的生活方式,宜采用普查方式
B.一組數據3,4,4,6,8,5的中位數是4
C.必然事件的概率是100%,隨機事件的概率大于0而小于1
D.若甲組數據的方差![]() =0.128,乙組數據的方差
=0.128,乙組數據的方差![]() =0.036,則甲組數據更穩定
=0.036,則甲組數據更穩定
查看答案和解析>>
科目:初中數學 來源: 題型:
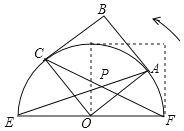
【題目】如圖,正方形OABC的邊長為2,以O為圓心,EF為直徑的半圓經過點A,連接AE、CF相交于點P.將正方形OABC從OA與OF重合的位置開始,繞著點O逆時針旋轉90°的過程中,線段OP的最小值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為4,點E,F分別在邊AB,AD上,且∠ECF=45°,CF的延長線交BA的延長線于點G,CE的延長線交DA的延長線于點H,連接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)線段AC,AG,AH什么關系?請說明理由;
(3)設AE=m,
①△AGH的面積S有變化嗎?如果變化.請求出S與m的函數關系式;如果不變化,請求出定值.
②請直接寫出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義[a,b,c]為函數y=ax2+bx+c的特征數,下面給出特征數為[2m,1﹣m,﹣1﹣m]的函數的一些結論,其中不正確的是( )
A. 當m=﹣3時,函數圖象的頂點坐標是(![]() ,
,![]() )
)
B. 當m>0時,函數圖象截x軸所得的線段長度大于![]()
C. 當m≠0時,函數圖象經過同一個點
D. 當m<0時,函數在x>![]() 時,y隨x的增大而減小
時,y隨x的增大而減小
查看答案和解析>>
科目:初中數學 來源: 題型:
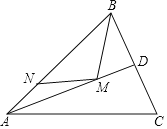
【題目】如圖,在銳角△ABC中,AB=5![]() ,∠BAC=45°,∠BAC的平分線交BC于點D,M,N分別是AD,AB上的動點,則BM+MN的最小值是______.
,∠BAC=45°,∠BAC的平分線交BC于點D,M,N分別是AD,AB上的動點,則BM+MN的最小值是______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com