
【題目】(14分)如圖,拋物線![]() 與x軸交于A,B兩點,與y軸交于點C,點D為拋物線的頂點,請解決下列問題.
與x軸交于A,B兩點,與y軸交于點C,點D為拋物線的頂點,請解決下列問題.

(1)填空:點C的坐標為( , ),點D的坐標為( , );
(2)設點P的坐標為(a,0),當![]() 最大時,求a的值并在圖中標出點P的位置;
最大時,求a的值并在圖中標出點P的位置;
(3)在(2)的條件下,將△BCP沿x軸的正方向平移得到△B′C′P′,設點C對應點C′的橫坐標為t(其中0<t<6),在運動過程中△B′C′P′與△BCD重疊部分的面積為S,求S與t之間的關系式,并直接寫出當t為何值時S最大,最大值為多少?
【答案】(1)C(0,3),D(1,4);(2)a=﹣3;(3)S=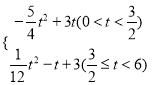 ,當t=
,當t=![]() 時,S有最大值
時,S有最大值![]() .
.
【解析】試題分析:(1)令x=0,得到C的坐標,把拋物線配成頂點式,可得頂點D的坐標;
(2)延長CD交x軸于點P.因為![]() 小于或等于第三邊CD,所以當
小于或等于第三邊CD,所以當![]() 等于CD時,
等于CD時, ![]() 的值最大.因此求出過CD兩點的解析式,求它與x軸交點坐標即可;
的值最大.因此求出過CD兩點的解析式,求它與x軸交點坐標即可;
(3)過C點作CE∥x軸,交DB于點E,求出直線BD的解析式,得到點E的坐標,求出P′C′與BC的交點M的坐標,分兩種情況討論:①點C′在線段CE上;②點C′在線段CE的延長線上,再分別求得N點坐標,再利用圖形的面積的差,可表示出S,再求得其最大值即可.
試題解析:(1)在![]() 中,令x=0,得到y=3,∴C(0,3),∵
中,令x=0,得到y=3,∴C(0,3),∵![]() =
=![]() ,∴D(1,4),故答案為:C(0,3),D(1,4);
,∴D(1,4),故答案為:C(0,3),D(1,4);
(2)∵在三角形中兩邊之差小于第三邊,∴延長DC交x軸于點P,設直線DC的解析式為![]() ,把D、C兩點坐標代入可得:
,把D、C兩點坐標代入可得: ![]() ,解得:
,解得: ![]() ,∴直線DC的解析式為
,∴直線DC的解析式為![]() ,將點P的坐標(a,0)代入得a+3=0,求得a=﹣3,如圖1,點P(﹣3,0)即為所求;
,將點P的坐標(a,0)代入得a+3=0,求得a=﹣3,如圖1,點P(﹣3,0)即為所求;
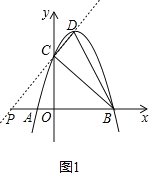
(3)過點C作CE∥x,交直線BD于點E,如圖2,
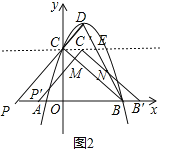
由(2)得直線DC的解析式為![]() ,易求得直線BD的解析式為
,易求得直線BD的解析式為![]() ,直線BC的解析式為
,直線BC的解析式為![]() ,在
,在![]() 中,當y=3時,x=
中,當y=3時,x=![]() ,∴E點坐標為(
,∴E點坐標為(![]() ,3),設直線P′C′與直線BC交于點M,∵P′C′∥DC,P′C′與y軸交于點(0,3﹣t),∴直線P′C′的解析式為
,3),設直線P′C′與直線BC交于點M,∵P′C′∥DC,P′C′與y軸交于點(0,3﹣t),∴直線P′C′的解析式為![]() ,聯立:
,聯立: ![]() ,解得:
,解得: 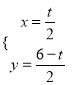 ,∴點M坐標為(
,∴點M坐標為(![]() ,
, ![]() ),∵B′C′∥BC,B′坐標為(3+t,0),∴直線B′C′的解析式為
),∵B′C′∥BC,B′坐標為(3+t,0),∴直線B′C′的解析式為![]() ,
,
分兩種情況討論:①當![]() 時,如圖2,B′C′與BD交于點N,聯立
時,如圖2,B′C′與BD交于點N,聯立![]() :,解得:
:,解得: ![]() ,∴N點坐標為(3﹣t,2t),S=S△B′C′P﹣S△BMP﹣S△BNB′=
,∴N點坐標為(3﹣t,2t),S=S△B′C′P﹣S△BMP﹣S△BNB′=![]() ×6×3﹣
×6×3﹣![]() (6﹣t)×
(6﹣t)×![]() (6﹣t)﹣
(6﹣t)﹣![]() t×2t=
t×2t=![]() ,其對稱軸為t=
,其對稱軸為t=![]() ,可知當
,可知當![]() 時,S隨t的增大而增大,當t=
時,S隨t的增大而增大,當t=![]() 時,有最大值
時,有最大值![]() ;
;
②當![]() 時,如圖3,直線P′C′與DB交于點N,
時,如圖3,直線P′C′與DB交于點N,
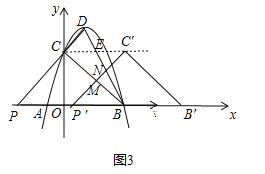
聯立: ![]() ,解得:
,解得: 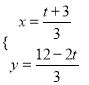 ,∴N點坐標為(
,∴N點坐標為(![]() ,
, ![]() ),S=S△BNP′﹣S△BMP′=
),S=S△BNP′﹣S△BMP′=![]() (6﹣t)×
(6﹣t)×![]() ﹣
﹣![]() ×(6﹣t)×
×(6﹣t)×![]() =
=![]() =
=![]() ;
;
顯然當![]() <t<6時,S隨t的增大而減小,當t=
<t<6時,S隨t的增大而減小,當t=![]() 時,S=
時,S=![]()
綜上所述,S與t之間的關系式為S=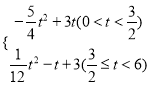 ,且當t=
,且當t=![]() 時,S有最大值,最大值為
時,S有最大值,最大值為![]() .
.
∵![]() ,∴當t=
,∴當t=![]() 時,S有最大值
時,S有最大值![]() .
.


科目:初中數學 來源: 題型:
【題目】蕪湖長江大橋是中國跨度最大的公路和鐵路兩用橋梁,大橋采用低塔斜拉橋橋型(如甲圖),圖乙是從圖甲引申出的平面圖,假設你站在橋上測得拉索AB與水平橋面的夾角是30°,拉索CD與水平橋面的夾角是60°,兩拉索頂端的距離BC為2米,兩拉索底端距離AD為20米,請求出立柱BH的長.(結果精確到0.1米, ![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題的逆命題成立的是( ).
A.全等三角形的對應角相等
B.若三角形的三邊滿足![]() ,則該三角形是直角三角形
,則該三角形是直角三角形
C.對頂角相等
D.同位角互補,兩直線平行
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,二次函數y1=(x﹣2)(x﹣4)的圖象與x軸交于A、B兩點(點A在點B的左側),其對稱軸l與x軸交于點C,它的頂點為點D.
(1)寫出點D的坐標 .
(2)點P在對稱軸l上,位于點C上方,且CP=2CD,以P為頂點的二次函數y2=ax2+bx+c(a≠0)的圖象過點A.
①試說明二次函數y2=ax2+bx+c(a≠0)的圖象過點B;
②點R在二次函數y1=(x﹣2)(x﹣4)的圖象上,到x軸的距離為d,當點R的坐標為 時,二次函數y2=ax2+bx+c(a≠0)的圖象上有且只有三個點到x軸的距離等于2d;
③如圖2,已知0<m<2,過點M(0,m)作x軸的平行線,分別交二次函數y1=(x﹣2)(x﹣4)y2=ax2+bx+c(a≠0)的圖象于點E、F、G、H(點E、G在對稱軸l左側),過點H作x軸的垂線,垂足為點N,交二次函數y1=(x﹣2)(x﹣4)的圖象于點Q,若△GHN∽△EHQ,求實數m的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】張明和李強兩名運動愛好者周末相約到東湖綠道進行跑步鍛煉.(1)周日早上6點,張明和李強同時從家出發,分別騎自行車和步行到離家距離分別為4.5千米和1.2千米的綠道落雁島入口匯合,結果同時到達,且張明每分鐘比李強每分鐘多行220米,求張明和李強的速度分別是多少米/分?
(1)兩人到達綠道后約定先跑 6 千米再休息,李強的跑步速度是張明跑步速度的m倍,兩人在同起點,同時出發,結果李強先到目的地n分鐘.
①當m=12,n=5時,求李強跑了多少分鐘?
②張明的跑步速度為 米/分(直接用含m,n的式子表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】機動車出發前油箱內有42升油,行駛若干小時后,途中在加油站加油若干升.油箱中余油量![]() (升)與行駛時間
(升)與行駛時間![]() (小時)之間的關系如圖所示,根據下圖回答問題:
(小時)之間的關系如圖所示,根據下圖回答問題:

(1)機動車行駛幾小時后加油?加了多少油?
(2)試求加油前油箱余油量![]() 與行駛時間
與行駛時間![]() 之間的關系式;
之間的關系式;
(3)如果加油站離目的地還有350千米,車速為60千米/小時,照這樣行駛,要到達目的地,油箱中的油是否夠用?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
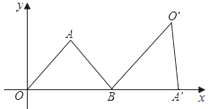
【題目】如圖,△AOB為等腰三角形,頂點A的坐標(2,![]() ),底邊OB在x軸上.將△AOB繞點B按順時針方向旋轉一定角度后得△A′O′B,點A的對應點A′在x軸上,則點O′的坐標為( )
),底邊OB在x軸上.將△AOB繞點B按順時針方向旋轉一定角度后得△A′O′B,點A的對應點A′在x軸上,則點O′的坐標為( )
A. (![]() ,
,![]() ) B. (
) B. (![]() ,
,![]() ) C. (
) C. (![]() ,
,![]() ) D. (
) D. (![]() ,4
,4![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,在平行四邊形ABCD中,BF平分![]() 交AD于點F,AE
交AD于點F,AE![]() BF于點O,交BC于點E,連接EF.
BF于點O,交BC于點E,連接EF.
(1)求證:四邊形ABEF是菱形;
(2)若AE=6,BF=8,CE=3,求四邊形ABCD的面積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com