“石頭、剪刀、布”是廣為流傳的游戲,游戲時比賽各方每次做“石頭”、“剪刀”、“布”三種手勢中的一種,規定“石頭”勝“剪刀”、“剪刀”勝“布”,“布”勝“石頭”,同種手勢或三種手勢循環不分勝負繼續比賽,假定甲、乙、丙三人每次都是等可能地做這三種手勢,那么:
(1)一次比賽中三人不分勝負的概率是多少?
(2)比賽中一人勝,二人負的概率是多少?
解:(1)分別用1,2,3表示“石頭”、“剪刀”、“布”三種手勢.
畫樹狀圖得:
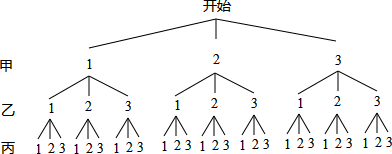
∵共有27種等可能的結果,一次比賽中三人不分勝負的9種情況,
∴一次比賽中三人不分勝負的概率是:
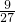
=

;
(2)∵比賽中一人勝,二人負的有6種情況,
∴比賽中一人勝,二人負的概率是:

=

.
分析:(1)首先分別用1,2,3表示“石頭”、“剪刀”、“布”三種手勢,然后根據題意畫樹狀圖,由樹狀圖即可求得所有等可能的結果與一次比賽中三人不分勝負的情況,再利用概率公式即可求得答案;
(2)由(1)即可求得比賽中一人勝,二人負的情況,再利用概率公式即可求得答案.
點評:本題考查的是用列表法或畫樹狀圖法求概率.列表法或畫樹狀圖法可以不重復不遺漏的列出所有可能的結果,列表法適合于兩步完成的事件,樹狀圖法適合兩步或兩步以上完成的事件.注意概率=所求情況數與總情況數之比.


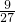 =
= ;
; =
= .
.
