
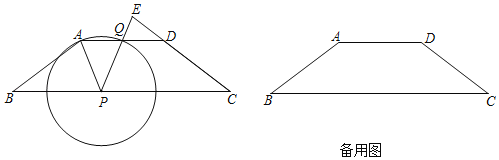
【題目】如圖,已知在梯形ABCD中,![]() ,P是線段BC上一點,以P為圓心,PA為半徑的
,P是線段BC上一點,以P為圓心,PA為半徑的![]() 與射線AD的另一個交點為Q,射線PQ與射線CD相交于點E,設
與射線AD的另一個交點為Q,射線PQ與射線CD相交于點E,設![]() .
.
(1)求證:![]() ;
;
(2)如果點Q在線段AD上(與點A、D不重合),設![]() 的面積為y,求y關于x的函數關系式,并寫出定義域;
的面積為y,求y關于x的函數關系式,并寫出定義域;
(3)如果![]() 與
與![]() 相似,求BP的長.
相似,求BP的長.
 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠B=90°,AB=20cm,BC=15cm,動點P從點A出發,以每秒4cm的速度沿AB方向運動,到達點B時停止運動.過點P作AB的垂線交斜邊AC于點E,將△APE繞點P順時針旋轉90°得到△DPF.設點P在邊AB上運動的時間為t(秒).

(1)當點F與點B重合時,求t的值;
(2)當△DPF與△ABC重疊部分的圖形為四邊形時,設此四邊形的面積為S,求S與t的函數關系式;
(3)若點M是DF的中點,當點M恰好在Rt△ABC的內角角平分線上時,求t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
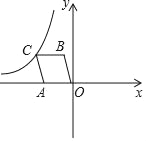
【題目】如圖A(﹣4,0),B(﹣1,3),以OA、OB為邊作OACB,經過A點的一次函數y=k1x+b與反比例函數y=![]() 的圖象交于點C.
的圖象交于點C.
(1)求一次函數y=k1x+b的解析式;
(2)請根據圖象直接寫出在第二象限內,當k1x+b>![]() 時,自變量x的取值范圍;
時,自變量x的取值范圍;
(3)將OACB向上平移幾個單位長度,使點A落在反比例函數的圖象上.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象交于點
的圖象交于點![]() ,且與
,且與![]() 軸交于點
軸交于點![]() ;點
;點![]() 在反比例函數
在反比例函數![]() 的圖象上,以點
的圖象上,以點![]() 為圓心,半徑為
為圓心,半徑為![]() 的作圓
的作圓![]() 與
與![]() 軸,
軸,![]() 軸分別相切于點
軸分別相切于點![]() 、
、![]() .
.

(1)求反比例函數和一次函數的解析式;
(2)請連結![]() ,并求出
,并求出![]() 的面積;
的面積;
(3)直接寫出當![]() 時,
時,![]() 的解集.
的解集.
查看答案和解析>>
科目:初中數學 來源: 題型:
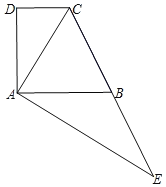
【題目】已知:如圖,梯形ABCD,DC∥AB,對角線AC平分∠BCD,點E在邊CB的延長線上,EA⊥AC,垂足為點A.
(1)求證:B是EC的中點;
(2)分別延長CD、EA相交于點F,若AC2=DCEC,求證:AD:AF=AC:FC.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,二次函數y=x2﹣2x+m(m>0)的對稱軸與比例系數為5的反比例函數圖象交于點A,與x軸交于點B,拋物線的圖象與y軸交于點C,且OC=3OB.

(1)求點A的坐標;
(2)求直線AC的表達式;
(3)點E是直線AC上一動點,點F在x軸上方的平面內,且使以A、B、E、F為頂點的四邊形是菱形,直接寫出點F的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
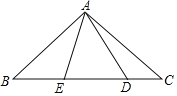
【題目】如圖,在Rt△ABC 中,AB=AC,D、E是斜邊BC上兩點,且∠DAE=45°,將△ADC繞點A順時針旋轉90°后,得到△AFB.設BE=a,DC=b,那么AB=_____.(用含a、b的式子表示AB)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某足球特色學校在商場購買甲、乙兩種品牌的足球.已知乙種足球比甲種足球每只貴20元,該校分別花費2000元、1400元購買甲、乙兩種足球,這樣購得甲種足球的數量是購得乙種足球數量的2倍,求甲、乙兩種足球的單價各是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,點
中,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的變換點
的變換點![]() 的坐標定義如下:
的坐標定義如下:
當![]() 時,點
時,點![]() 的坐標為
的坐標為![]() ;當
;當![]() 時,點
時,點![]() 的坐標為
的坐標為![]() .
.
(1)點![]() 的變換點
的變換點![]() 的坐標是 ;點
的坐標是 ;點![]() 的變換點為
的變換點為![]() ,連接
,連接![]() ,則
,則![]() °;
°;
(2)已知拋物線![]() 與
與![]() 軸交于點
軸交于點![]() ,
,![]() (點
(點![]() 在點
在點![]() 的左側),頂點為
的左側),頂點為![]() .點
.點![]() 在拋物線
在拋物線上,點
![]() 的變換點為
的變換點為![]() .若點
.若點![]() 恰好在拋物線的對稱軸上,且四邊形
恰好在拋物線的對稱軸上,且四邊形![]() 是菱形,求
是菱形,求![]() 的值;
的值;
(3)若點![]() 是函數
是函數![]() 圖象上的一點,點
圖象上的一點,點![]() 的變換點為
的變換點為![]() ,連接
,連接![]() ,以
,以![]() 為直徑作
為直徑作![]() ,
,![]() 的半徑為
的半徑為![]() ,請直接寫出
,請直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com