
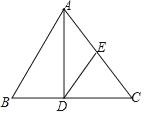
【題目】已知:如圖,在△ABC中,AD是邊BC上的高,E為邊AC的中點(diǎn),BC=21,AD=8,sinB=![]() .
.
求:(1)線段DC的長(zhǎng);
(2)tan∠EDC的值.
【答案】(1)15;(2)![]()
【解析】
第(1)問(wèn)中要求CD的長(zhǎng),已知條件中給出了BC的長(zhǎng),這時(shí)只要求出BD的長(zhǎng)即可;
利用三角函數(shù)的定義和AD的長(zhǎng)可以得到AB的長(zhǎng),再在Rt△ABD中利用勾股定理得到BD的長(zhǎng),繼而求出CD的長(zhǎng);
第(2)問(wèn)是求一個(gè)銳角的正切值,需要放在直角三角形中求解,因此,要求tan∠CDE的值,就需將∠CDE進(jìn)行轉(zhuǎn)化;
利用直角三角形斜邊上的中線可以得到DE=EC,進(jìn)而得到∠EDC=∠ECD,從而將問(wèn)題轉(zhuǎn)化為求∠EDC的正切值.
解:(1)∵AD是BC邊上的高,△ABD和△ACD是直角三角形,
在Rt△ABD中,∵sinB=![]() ,AD=8,
,AD=8,
∴![]() =
=![]() ,
,
∴AB=10,
∴BD=![]() =6,
=6,
又∵BC=21,
∴CD=BC﹣BD=15;
(2)在Rt△ACD中,
∵E為斜邊AC的中點(diǎn),
∴ED=EC=![]() AC,
AC,
∴∠C=∠EDC,
∴tan∠EDC=tanC=![]() =
=![]() .
.


 學(xué)而優(yōu)暑期銜接南京大學(xué)出版社系列答案
學(xué)而優(yōu)暑期銜接南京大學(xué)出版社系列答案 Happy holiday歡樂(lè)假期暑假作業(yè)廣東人民出版社系列答案
Happy holiday歡樂(lè)假期暑假作業(yè)廣東人民出版社系列答案 快樂(lè)暑假暑假能力自測(cè)中西書(shū)局系列答案
快樂(lè)暑假暑假能力自測(cè)中西書(shū)局系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知O為坐標(biāo)原點(diǎn),A,B分別在y軸、x軸正半軸上,D是x軸正半軸上一動(dòng)點(diǎn),AD=DE,∠ADE=α,矩形AOBC的面積為32且AC=2BC.
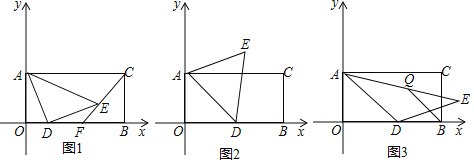
(1)如圖1,當(dāng)α=90°時(shí),直線CE交x軸于點(diǎn)F,求證:F為OB中點(diǎn);
(2)如圖2,當(dāng)α=60°時(shí),若D是OB中點(diǎn),求E點(diǎn)坐標(biāo);
(3)如圖3,當(dāng)α=120°時(shí),Q是AE的中點(diǎn),求D點(diǎn)運(yùn)動(dòng)過(guò)程中BQ的最小值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
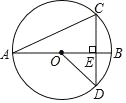
【題目】如圖,線段 AB 是⊙O 的直徑,弦 CD⊥AB,AB=8,∠CAB=22.5°,則 CD的長(zhǎng)等于___________________________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,正方形ABCD的頂點(diǎn)B,C在x軸的正半軸上,反比例函數(shù)y=![]() (k≠0)在第一象限的圖象經(jīng)過(guò)頂點(diǎn)A(m,2)和CD邊上的點(diǎn)E(n,
(k≠0)在第一象限的圖象經(jīng)過(guò)頂點(diǎn)A(m,2)和CD邊上的點(diǎn)E(n,![]() ),過(guò)點(diǎn)E的直線l交x軸于點(diǎn)F,交y軸于點(diǎn)G(0,-2),則點(diǎn)F的坐標(biāo)是( )
),過(guò)點(diǎn)E的直線l交x軸于點(diǎn)F,交y軸于點(diǎn)G(0,-2),則點(diǎn)F的坐標(biāo)是( )

A. (![]() ,0)B. (
,0)B. (![]() ,0)C. (
,0)C. (![]() ,0)D. (
,0)D. (![]() ,0)
,0)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】重慶八中渝北校區(qū)前的同茂大道![]() 的路有一座小山
的路有一座小山![]() ,因工程開(kāi)發(fā)需要爆破.小山
,因工程開(kāi)發(fā)需要爆破.小山![]() 北偏東
北偏東![]() 方向,距小山
方向,距小山![]() 米的
米的![]() 處是同茂大道中央公園東公交站;小山北偏西
處是同茂大道中央公園東公交站;小山北偏西![]() 方向,距小山
方向,距小山![]() 米的
米的![]() 處是同茂大道上麗山公交站.
處是同茂大道上麗山公交站.
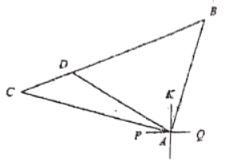
(1)爆破時(shí),在爆破點(diǎn)![]() 周圍
周圍![]() 米范圍有危險(xiǎn)請(qǐng)問(wèn),為了安全,在爆破小山時(shí)需不需要暫時(shí)封閉同茂大道
米范圍有危險(xiǎn)請(qǐng)問(wèn),為了安全,在爆破小山時(shí)需不需要暫時(shí)封閉同茂大道![]() ?請(qǐng)通過(guò)計(jì)算說(shuō)明理由;
?請(qǐng)通過(guò)計(jì)算說(shuō)明理由;
(2)點(diǎn)![]() 是同茂大道
是同茂大道![]() 上一點(diǎn)(點(diǎn)
上一點(diǎn)(點(diǎn)![]() 不與點(diǎn)
不與點(diǎn)![]() 重合),
重合),![]() ,
,![]() 區(qū)域是規(guī)劃中的公園,問(wèn):這個(gè)公園占地多少平方米?
區(qū)域是規(guī)劃中的公園,問(wèn):這個(gè)公園占地多少平方米?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
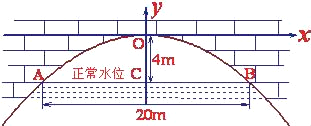
【題目】有一座拋物線形拱橋,正常水位時(shí)橋下水面寬度為20m,拱頂距離水面4m.
(1)在如圖所示的直角坐標(biāo)系中,求出該拋物線的解析式;
(2)設(shè)正常水位時(shí)橋下的水深為2m,為保證過(guò)往船只順利航行,橋下水面的寬度不得小于18m,求水深超過(guò)多少米時(shí)就會(huì)影響過(guò)往船只在橋下的順利航行.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
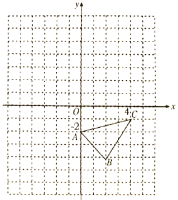
(1)請(qǐng)畫出![]() 關(guān)于
關(guān)于![]() 軸對(duì)稱的
軸對(duì)稱的![]() (其中
(其中![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() ,
,![]() 的對(duì)稱點(diǎn),不寫畫法,寫出
的對(duì)稱點(diǎn),不寫畫法,寫出![]() 、
、![]() 、
、![]() 的坐標(biāo))
的坐標(biāo))
(2)在![]() 軸上是否存在一點(diǎn)
軸上是否存在一點(diǎn)![]() ,使
,使![]() 的值最小,若有,請(qǐng)作出點(diǎn)
的值最小,若有,請(qǐng)作出點(diǎn)![]() ,并直接寫出
,并直接寫出![]() 點(diǎn)的坐標(biāo),若沒(méi)有,請(qǐng)說(shuō)明理由.
點(diǎn)的坐標(biāo),若沒(méi)有,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知關(guān)于![]() 的方程:
的方程:![]() .
.
(1)如果此方程只有一個(gè)實(shí)數(shù)根,求![]() 的值;
的值;
(2)如果此方程有兩個(gè)實(shí)數(shù)根,求![]() 的取值范圍;
的取值范圍;
(3)如果此方程無(wú)實(shí)數(shù)根,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
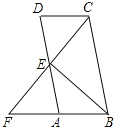
【題目】如圖,在平行四邊形ABCD中,點(diǎn)E為AD的中點(diǎn),延長(zhǎng)CE交BA的延長(zhǎng)線于點(diǎn)F.
(1)求證:AB=AF;
(2)若BC=2AB,∠BCD=100°,求∠ABE的度數(shù).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com