【題目】如圖，正比例函數 
的圖象與反比例函數 
的圖象交于A、B兩點，點C在x軸負半軸上，AC＝AO，△ACO的面積為12．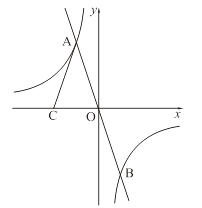
（1）求k的值；
（2）根據圖象，當 
時，寫出自變量 
的取值范圍．
【答案】
（1）
解：如圖，過點A作AD⊥OC于點D.
又∵AC=AO.
∴CD=DO.
∴S△ADO=
S△ACO=6.
∴k=-12.
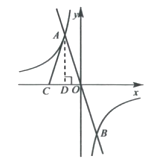
（2）
解：由圖像可知：χ＜-2或0＜χ＜2.
【解析】（1）如圖，過點A作AD⊥OC于點D，根據等腰三角形的性質可以得出S△ADO=
S△ACO=6；從而求出k的值.
（2）從圖像可以得出答案.
【考點精析】解答此題的關鍵在于理解反比例函數的性質的相關知識，掌握性質:當k＞0時雙曲線的兩支分別位于第一、第三象限，在每個象限內y值隨x值的增大而減小； 當k＜0時雙曲線的兩支分別位于第二、第四象限，在每個象限內y值隨x值的增大而增大，以及對比例系數k的幾何意義的理解，了解幾何意義：表示反比例函數圖像上的點向兩坐標軸所作的垂線段與兩坐標軸圍成的矩形的面積．
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，AD是∠BAC的平分線．若P，Q分別是AD和AC上的動點，則PC+PQ的最小值是（ ）
A. 
B. 4 C. 
D. 5
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一個粒子在第一象限內及x軸、y軸上運動，在第一分鐘，它從原點運動到點(1，0)，第二分鐘，它從點(1，0)運動到點(1，1)，而后它接著按圖中箭頭所示在與x軸，y軸平行的方向上來回運動，且每分鐘移動1個單位長度，那么在第2019分鐘時，這個粒子所在位置的坐標是( )
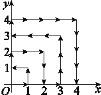
A. (44，5) B. (5，44) C. (44，6) D. (6，44)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，直線y=-x+m分別交于x軸、y軸于A，B兩點，已知點C（2，0）.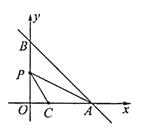
（1）當直線AB經過點C時，點O到直線AB的距離是；
（2）設點P為線段OB的中點，連結PA，PC,若∠CPA=∠ABO，則m的值是.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】(本題6分)如圖，在平面直角坐標系中，△ABC各頂點的坐標分別為A(2，2)，B(4,1），C(4,4)．
（1）作出 
ABC關于原點O成中心對稱的 A1B1C1.
（2）作出點A關于x軸的對稱點A'.若把點A'向右平移a個單位長度后落在 A1B1C1的內部（不包括頂點和邊界），求a的取值范圍.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下列材料：
∵
，
，
，……
，
∴
=
=
=
．
解答下列問題：
（1）在和式
中，第6項為______，第n項是__________．
（2）上述求和的想法是通過逆用________法則，將和式中的各分數轉化為兩個數之差，使得除首末兩項外的中間各項可以_______，從而達到求和的目的．
（3）受此啟發，請你解下面的方程：
．
查看答案和解析>>
科目：初中數學 來源： 題型：
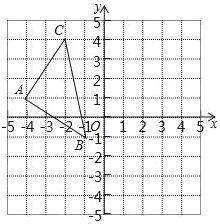
【題目】已知，△ABC在平面直角坐標系中的位置如圖所示．
（1）把△ABC向下平移2個單位長度得到△A1B1C1，請畫出△A1B1C1；
（2）請畫出△A1B1C1關于y軸對稱的△A2B2C2，并寫出A2的坐標；
（3）求△ABC的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】化簡．
(1)( x- y)( x+ y) ( x2+ y2) ( x4+ y4)·…·(x16+ y16)；
(2)(22+1)(24+1)(28+1)(216+1)．
查看答案和解析>>
科目：初中數學 來源： 題型：
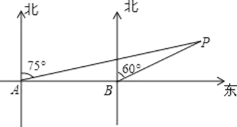
【題目】如圖，某輪船由西向東航行，在 A 處測得小島 P 的方位是北偏東 75°，又繼續航行 8 海里后，在 B 處測得小島 P 的方位是北偏東 60°，則此時△ABP 的面積為______平方海里．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com