
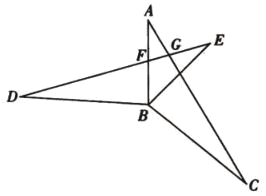
【題目】如圖,已知![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于點
于點![]() ,
,![]() 交
交![]() 于點
于點![]() .
.
(1)求證:![]() ;
;
(2)當![]() 時,證明四邊形
時,證明四邊形![]() 是菱形;
是菱形;
(3)若![]() 的外心在其內部,
的外心在其內部,![]() ,直接寫出
,直接寫出![]() 的值.
的值.
【答案】(1)見解析 (2)見解析 (3)160
【解析】
(1)利用AAS定理證明△ABC≌△EBD;
(2)根據平行線的判定定理得到AC∥BD,DE∥BC,得到四邊形BDGC為平行四邊形,根據菱形的判定定理證明即可;
(3)根據△DFB的外心在其內部時,△DFB為銳角三角形解答.
(1)證明:在△ABC和△EBD中,
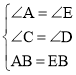 ,
,
∴△ABC≌△EBD(AAS);
(2)證明:∵△ABC≌△EBD,
∴BC=BD,∠ABC=∠DBE=130°,
∵∠ABE=100°,
∴∠ABD=∠CBE=30°,
∴∠ABD=∠A,∠EBC=∠E,
∴AC∥BD,DE∥BC,
∴四邊形BDGC為平行四邊形,
∵BD=BC,
∴四邊形BDGC是菱形;
(3)解:△DFB的外心在其內部時,△DFB為銳角三角形,
當BF⊥DE時,n=90,
當BF⊥BD時,m=70,
∴m+n=160.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是射線
是射線![]() 上一點,連接
上一點,連接![]() ,沿
,沿![]() 將三角形
將三角形![]() 折疊,得三角形
折疊,得三角形![]() .
.
(1)當![]() 時,
時,![]() =_______度;
=_______度;
(2)如圖,當![]() 時,求線段
時,求線段![]() 的長度;
的長度;

(3)當點![]() 落在平行四邊形
落在平行四邊形![]() 的邊上時,直接寫出線段
的邊上時,直接寫出線段![]() 的長度.
的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在⊙O中,AB為直徑,點C為圓上一點,將劣弧![]() 沿弦AC翻折交AB于點D,連結CD.如圖,若點D與圓心O不重合,∠BAC=25°,則∠DCA的度數( )
沿弦AC翻折交AB于點D,連結CD.如圖,若點D與圓心O不重合,∠BAC=25°,則∠DCA的度數( )

A.35°B.40°C.45°D.65°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在OABC中,以O為圓心,OA為半徑的圓與BC相切于點B,與OC相交于點D,點E在⊙O上,連接CE與⊙O交于點F.

(1)若BC=20,求![]() 的長度;
的長度;
(2)若EF=AB,求∠OCE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】飲料廠生產某品牌的飲料成本是每瓶5元,每天的生產量不超過9000瓶.根據市場調查,以單價8元批發(fā)給經銷商,經銷商每天愿意經銷5000瓶,并且表示單價每降價0.1元,經銷商每天愿意多經銷500瓶.
(1)求出飲料廠每天的利潤![]() (元)與批發(fā)單價
(元)與批發(fā)單價![]() (元)之間的函數關系式;
(元)之間的函數關系式;
(2)批發(fā)單價定為多少元時,飲料廠每天的利潤最大,最大利潤是多少元;
(3)如果該飲料廠要使每天的利潤不低于18750元,且每天的總成本不超過42500元,那么批發(fā)單價應控制在什么范圍.(每天的總成本![]() 每瓶的成本
每瓶的成本![]() 每天的經銷量)
每天的經銷量)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校開發(fā)了“書畫、器樂、戲曲、棋類”四大類興趣課程.為了解全校學生對每類課程的選擇情況,隨機抽取了若干名學生進行調查(每人必選且只能選一類),先將調查結果繪制成如下兩幅不完整的統(tǒng)計圖:
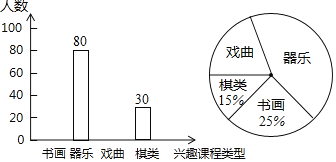
(1)本次隨機調查了多少名學生?
(2)補全條形統(tǒng)計圖中“書畫”、“戲曲”的空缺部分;
(3)若該校共有![]() 名學生,請估計全校學生選擇“戲曲”類的人數;
名學生,請估計全校學生選擇“戲曲”類的人數;
(4)學校從這四類課程中隨機抽取兩類參加“全市青少年才藝展示活動”,用樹形圖或列表法求處恰好抽到“器樂”和“戲曲”類的概率.(書畫、器樂、戲曲、棋類可分別用字幕![]() 表示)
表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,AB=4,C為半圓AB的中點,P為![]() 上一動點,延長BP至點Q,使BPBQ=AB2.若點P由A運動到C,則點Q運動的路徑長為_____.
上一動點,延長BP至點Q,使BPBQ=AB2.若點P由A運動到C,則點Q運動的路徑長為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把正方形鐵片OABC置于平面直角坐標系中,頂點A的坐標為(3,0),點P(1,2)在正方形鐵片上,將正方形鐵片繞其右下角的頂點按順時針方向依次旋轉90°,第一次旋轉至圖①位置,第二次旋轉至圖②位置……,則正方形鐵片連續(xù)旋轉2020次后,點P的坐標為__________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為進一步提升教育教學質量,調動學生學習的興趣,某校在七年級學生中開展了對語文、數學、英語、歷史、地理這五門課程的興趣愛好情況的調查,以便采取必要教學改革,激發(fā)學生對各學科的興趣愛好.隨機選取該年級部分學生進行調查,要求每名學生從中選出一門最感興趣的課程(每名學生只能選一門,不能多選),以下是根據調查結果繪制的不完整統(tǒng)計圖表:
課程代號 |
|
|
|
|
|
課程名稱 | 語文 | |數學 | 英語 | 歷史 | 地理 |
最感興趣人數 | 12 | 30 |
| 54 | 9 |
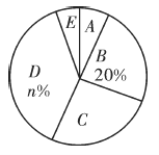
請你根據以上信息,解答下列問題:
(1)被調查學生的總數為______人,![]() ______,
______,![]() ______;
______;
(2)被調查學生中,最喜愛課程的“眾數”是______;
(3)若該年級共有800名學生,請估計該年級對語文最感興趣的學生人數.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com