
【題目】如圖,數軸上有A、B、C三個點,它們表示的數分別是![]() 、
、![]() 、
、![]() 。
。

(1)填空:AB= ,BC= ;
(2)現有動點M、N都從A點出發,點M以每秒2個單位長度的速度向右移動,當點M移動到B點時,點N才從A點出發,并以每秒3個單位長度的速度向右移動,求點N移動多少時間,點N追上點M?
(3)若點A以每秒1個單位長度的速度向左運動,同時,點B和點C分別以每秒3個單位長度和7個單位長度的速度向右運動。試探索:BC-AB的值是否隨著時間的變化而改變?請說明理由。
【答案】(1) AB=15,BC=20;(2) 點N移動15秒時,點N追上點M;(3) BC-AB的值不會隨著時間的變化而改變,理由見解析
【解析】
(1)根據數軸上點的位置求出AB與BC的長即可,
(2)不變,理由為:經過t秒后,A、B、C三點所對應的數分別是-24-t,-10+3t,10+7t,表示出BC,AB,求出BC-AB即可做出判斷,
(3)經過t秒后,表示P、Q兩點所對應的數,根據題意列出關于t的方程,求出方程的解得到t的值,分三種情況考慮,分別求出滿足題意t的值即可.
解:(1)AB=15,BC=20,
(2)設點N移動![]() 秒時,點N追上點M,由題意得:
秒時,點N追上點M,由題意得:

![]() ,
,
解得![]() ,
,
答:點N移動15秒時,點N追上點M.
(3)設運動時間是![]() 秒,那么運動后A、B、C三點表示的數分別是
秒,那么運動后A、B、C三點表示的數分別是![]() 、
、![]() 、
、![]() ,
,
∴BC![]() ,AB
,AB![]() ,
,
∴BC-AB![]() ,
,
∴BC-AB的值不會隨著時間的變化而改變.


科目:初中數學 來源: 題型:
【題目】如圖1,我們把對角線互相垂直的四邊形叫做垂美四邊形.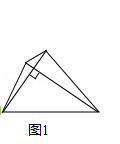
(1)概念理解:如圖2,在四邊形ABCD中,AB=AD,CB=CD,問四邊形ABCD是垂美四邊形嗎?請說明理由.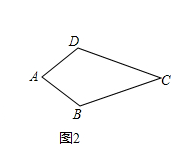
(2)性質探究:試探索垂美四邊形ABCD兩組對邊AB,CD與BC,AD之間的數量關系.
猜想結論:(要求用文字語言敘述) ![]()
寫出證明過程(先畫出圖形,寫出已知、求證).
(3)問題解決:如圖3,分別以Rt△ACB的直角邊AC和斜邊AB為邊向外作正方形ACFG和正方形ABDE,連接CE,BG,GE,已知AC=4,AB=5,求GE長.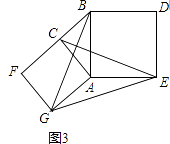
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知E、F分別為正方形ABCD的邊AB,BC的中點,AF與DE交于點M,O為BD的中點,則下列結論:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM= ![]() MF.其中正確結論的個數是( )
MF.其中正確結論的個數是( ) 
A.5個
B.4個
C.3個
D.2個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB是⊙O的直徑,點P在BA的延長線上,PD切⊙O于點D,過點B作BE垂直于PD,交PD的延長線于點C,連接AD并延長,交BE于點E. 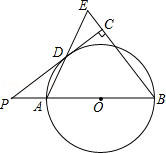
(1)求證:AB=BE;
(2)若PA=2,cosB= ![]() ,求⊙O半徑的長.
,求⊙O半徑的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,已知線段AB,點C分線段AB為5∶7,點D分線段AB為5∶11,若AB=96cm,求線段CD的長。
(2)如圖2,已知線段AB上有C、D兩點,AC=![]() BC,AD=
BC,AD=![]() BD,CD=14cm,求線段AB的長。
BD,CD=14cm,求線段AB的長。
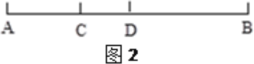
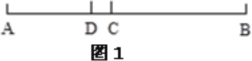
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知數軸上三點M,O,N對應的數分別為-1,0,3,點P為數軸上任意一點,其對應的數為x.
![]()
(1)MN的長為 ;
(2)如果點P到點M、點N的距離相等,那么x的值是 ;
(3)數軸上是否存在點P,使點P到點M、點N的距離之和是8?若存在,直接寫出x的值;若不存在,請說明理由.
(4)如果點P以每分鐘1個單位長度的速度從點O向左運動,同時點M和點N分別以每分鐘2個單位長度和每分鐘3個單位長度的速度也向左運動.設t分鐘時點P到點M、點N的距離相等,求t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料并解決有關問題:
我們知道:|x|= .現在我們可以用這一結論來化簡含有絕對值的代數式,現在我們可以用這一結論來化簡含有絕對值的代數式,如化簡代數式|x+1|+|x﹣2|時,可令x+1=0和x﹣2=0,分別求得x=﹣1,x=2(稱﹣1,2分別為|x+1|與|x﹣2|的零點值).在實數范圍內,零點值x=﹣1和,x=2可將全體實數分成不重復且不遺漏的如下3種情況:
.現在我們可以用這一結論來化簡含有絕對值的代數式,現在我們可以用這一結論來化簡含有絕對值的代數式,如化簡代數式|x+1|+|x﹣2|時,可令x+1=0和x﹣2=0,分別求得x=﹣1,x=2(稱﹣1,2分別為|x+1|與|x﹣2|的零點值).在實數范圍內,零點值x=﹣1和,x=2可將全體實數分成不重復且不遺漏的如下3種情況:
①x<﹣1;②﹣1≤x<2;③x≥2.
從而化簡代數式|x+1|+|x﹣2|可分以下3種情況:
①當x<﹣1時,原式=﹣(x+1)﹣(x﹣2)=﹣2x+1;
②當﹣1≤x<2時,原式=x+1﹣(x﹣2)=3;
③當x≥2時,原式=x+1+x﹣2=2x﹣1.綜上討論,原式= .
.
通過以上閱讀,請你解決以下問題:
(1)化簡代數式|x+2|+|x﹣4|.
(2)求|x﹣1|﹣4|x+1|的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法中正確的是( )
A. 若|a|=﹣a,則 a 一 定是負數
B. 單項式 x3y2z 的系數為 1,次數是 6
C. 若 AP=BP,則點 P 是線段 AB 的中點
D. 若∠AOC=![]() ∠AOB,則射線 OC 是∠AOB 的平分線
∠AOB,則射線 OC 是∠AOB 的平分線
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com