
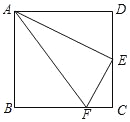
【題目】如圖,在正方形ABCD中,點E是CD的中點,點F是BC上的一點,且BF=3CF,連接AE、AF、EF,下列結論:①△ADE∽△ECF,②∠DAE=∠EAF,③AE2=ADAF,④S△AEF=5S△ECF,其中正確結論的個數是( )
A. 1個B. 2個C. 3個D. 4個
【答案】D
【解析】
】設正方形的邊長為4a,根據題意用a表示出FC,BF,CE,DE,根據相似三角形的判定定理,勾股定理,正切的定義,相似三角形的性質定理判斷即可.
設正方形的邊長為4a,
則FC=a,BF=3a,CE=DE=2a,
∴![]() =2,
=2,![]() =2,
=2,
∴![]() ,又∠D=∠C,
,又∠D=∠C,
∴△ADE∽△ECF,①正確;
由勾股定理得,EF=![]() ,AE=
,AE=![]() ,
,
AF=![]() ,
,
tan∠DAE=![]() ,tan∠EAF=
,tan∠EAF=![]() ,
,
∴∠DAE=∠EAF,②正確;
AE2=(2![]() a)2=20a2,ADAF=4a5a=20a2,
a)2=20a2,ADAF=4a5a=20a2,
∴AE2=ADAF,③正確;
∵AE2=ADAF,
∴![]() ,又∠DAE=∠EAF,
,又∠DAE=∠EAF,
∴△ADE∽△AEF,
∴△ECF∽△AEF,
∴![]() =5,
=5,
∴S△AEF=5S△ECF,⑤正確;
故選:D.


 教學練新同步練習系列答案
教學練新同步練習系列答案 課前課后同步練習系列答案
課前課后同步練習系列答案科目:初中數學 來源: 題型:
【題目】某校計劃一次性購買排球和籃球,每個籃球的價格比排球貴30元;購買2個排球和3個籃球共需340元.
(1)求每個排球和籃球的價格:
(2)若該校一次性購買排球和籃球共60個,總費用不超過3800元,且購買排球的個數少于39個.設排球的個數為m,總費用為y元.
①求y關于m的函數關系式,并求m可取的所有值;
②在學校按怎樣的方案購買時,費用最低?最低費用為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四川省蘆山縣4月20日發生了7.0級強烈地震,政府為了盡快搭建板房安置災民,給某廠下達了生產A種板材48000m2和B種板材24000m2的任務.
⑴如果該廠安排280人生產這兩種板材,每人每天能生產A種板材60 m2或B種板材40 m2,請問:應分別安排多少人生產A種板材和B種板材,才能確保同時完成各自的生產任務?
⑵某災民安置點計劃用該廠生產的兩種板材搭建甲、乙兩種規格的板房共400間,已知建設一間甲型板房和一間乙型板房所需板材及安置人數如下表所示:
板房 | A種板材(m2) | B種板材(m2) | 安置人數 |
甲型 | 110 | 61 | 12 |
乙型 | 160 | 53 | 10 |
①共有多少種建房方案可供選擇?
②若這個災民安置點有4700名災民需要安置,這400間板房能否滿足需要?若不能滿足請說明理由;若能滿足,請說明應選擇什么方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,△ABC 頂點 A(2,3).若以原點 O 為位似中心,畫三角形 ABC
的位似圖形△A′B′C′,使△ABC 與△A′B′C′的相似比為![]() ,則 A′的坐標為( )
,則 A′的坐標為( )
A. (3,![]() ) B. (
) B. (![]() ,6) C. (3,
,6) C. (3,![]() )或(-3,-
)或(-3,-![]() ) D. (
) D. (![]() ,6)或(-
,6)或(-![]() ,-6)
,-6)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】邊長為6的等邊△ABC中,點D、E分別在AC、BC邊上,DE∥AB,EC=2![]() .
.
(1)如圖1,將△DEC沿射線EC方向平移,得到△D′E′C′,邊D′E′與AC的交點為M,邊C′D′與∠ACC′的角平分線交于點N,當CC′多大時,四邊形MCND′為菱形?并說明理由.
(2)如圖2,將△DEC繞點C旋轉∠α(0°<α<360°),得到△D′E′C,連接AD′、BE′.邊D′E′的中點為P.
①在旋轉過程中,AD′和BE′有怎樣的數量關系?并說明理由;
②連接AP,當AP最大時,求AD′的值.(結果保留根號)
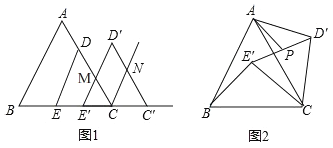
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在水果銷售旺季,某水果店購進一優質水果,進價為20元/千克,售價不低于20元/千克,且不超過32元/千克,根據銷售情況,發現該水果一天的銷售量y(千克)與該天的售價x(元/千克)滿足如下表所示的一次函數關系.
銷售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售價x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天這種水果的售價為23.5元/千克,求當天該水果的銷售量.
(2)如果某天銷售這種水果獲利150元,那么該天水果的售價為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知:AB為⊙O直徑,PQ與⊙O交于點C,AD⊥PQ于點D,且AC為∠DAB的平分線,BE⊥PQ于點E.
(1)求證:PQ與⊙O相切;
(2)求證:點C是DE的中點.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】不透明的口袋里裝有紅、黃、藍三種顏色的小球(除顏色不同外,其它都一樣),其中紅球2個,藍球1個,現在從中任意摸出一個紅球的概率為![]() .
.
(1)求袋中黃球的個數;
(2)第一次摸出一個球(不放回),第二次再摸出一個球,請用樹狀圖或列表法求兩次摸出的都是紅球的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在湖邊高出水面40m的山頂A處看見一架無人機停留在湖面上空某處,觀察到無人機底部標志P處的仰角為45°,又觀其在湖中之像的俯角為60°,則無人機底部P距離湖面的高度是( )
A. (40![]() +40)mB. (40
+40)mB. (40![]() +80)mC. (50
+80)mC. (50![]() +100)mD. (50
+100)mD. (50![]() +50)m
+50)m
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com