
【題目】下列各數(shù)中,最小的數(shù)是( )
A.﹣2
B.﹣0.1
C.0
D.|﹣1|
【答案】A
【解析】解:因為正實數(shù)都大于0, 所以 ![]() >0,
>0,
又因為正實數(shù)大于一切負實數(shù),
所以 ![]() >﹣2,
>﹣2,
所以 ![]() >﹣0.1
>﹣0.1
所以 ![]() 最大,
最大,
故D不對;
又因為負實數(shù)都小于0,
所以0>﹣2,0>﹣0.1,
故C不對;
因為兩個負實數(shù)絕對值大的反而小,
所以﹣2<﹣0.1,
故B不對;
故選A.
【考點精析】認真審題,首先需要了解有理數(shù)大小比較(有理數(shù)比大小:1、正數(shù)的絕對值越大,這個數(shù)越大2、正數(shù)永遠比0大,負數(shù)永遠比0小3、正數(shù)大于一切負數(shù)4、兩個負數(shù)比大小,絕對值大的反而小5、數(shù)軸上的兩個數(shù),右邊的數(shù)總比左邊的數(shù)大6、大數(shù)-小數(shù) > 0,小數(shù)-大數(shù) < 0).


 小天才課時作業(yè)系列答案
小天才課時作業(yè)系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導(dǎo)學(xué)系列答案
新輔教導(dǎo)學(xué)系列答案 陽光同學(xué)一線名師全優(yōu)好卷系列答案
陽光同學(xué)一線名師全優(yōu)好卷系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知某船于上午8時在A處觀測小島C在北偏東60°方向上,該船以每小時20海里的速度向東航行到B處,測得小島C在北偏東30°方向上,船以原來的速度繼續(xù)向東航行2小時,到達島C正南方點D處,船從A到D一共航行了多少海里?

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】七年級學(xué)生小聰和小明完成了數(shù)學(xué)實驗《鐘面上的數(shù)學(xué)》之后,自制了一個模擬鐘面,如圖所示,O為模擬鐘面圓心,M、O、N在一條直線上,指針OA、OB分別從OM、ON出發(fā)繞點O轉(zhuǎn)動,OA運動速度為每秒15°,OB運動速度為每秒5°,當(dāng)一根指針與起始位置重合時,運動停止,設(shè)轉(zhuǎn)動的時間為t秒,請你試著解決他們提出的下列問題:
(1)若OA順時針轉(zhuǎn)動,OB逆時針轉(zhuǎn)動,t= 秒時,OA與OB第一次重合;
(2)若它們同時順時針轉(zhuǎn)動,
①當(dāng) t=2秒時,∠AOB= °;
②當(dāng)t為何值時,OA與OB第一次重合?
③當(dāng)t為何值時,∠AOB=30°?

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】我國南水北調(diào)中線工程的起點是丹江水庫,按照工程計劃,需對原水庫大壩進行混凝土加高,使壩高由原來的162米增加到176.6米,以抬高蓄水位.如圖是某一段壩體加高工程的截面示意圖,其中原壩體的高為BE,背水坡坡角∠BAE=68°,新壩體的高為DE,背水坡坡角∠DCE=60°.求工程完工后背水坡坡底端水平方向增加的寬度AC(結(jié)果精確到0.1米.參考數(shù)據(jù):sin68°≈0.93,cos68°≈0.37,tan68°≈2.50, ![]() ).
).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某學(xué)校為了加強訓(xùn)練學(xué)生的籃球和足球運球技能,準備購買一批籃球和足球用于訓(xùn)練,已知1個籃球和2個足球共需116元;2個籃球和3個足球共需204元
![]() 求購買1個籃球和1個足球各需多少元?
求購買1個籃球和1個足球各需多少元?
![]() 若學(xué)校準備購進籃球和足球共40個,并且總費用不超過1800元,則籃球最多可購買多少個?
若學(xué)校準備購進籃球和足球共40個,并且總費用不超過1800元,則籃球最多可購買多少個?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】點A在數(shù)軸上對應(yīng)的數(shù)為a,點B對應(yīng)的數(shù)為b,且a,b滿足:|a+3|+(b-2)2=0
(1)求線段AB的長;
(2)如圖①,點C在數(shù)軸上對應(yīng)的數(shù)為x,且是方程![]() 的根,在數(shù)軸上是否存在點M使MA+MB=
的根,在數(shù)軸上是否存在點M使MA+MB=![]() BC+AB?若存在,求出點M對應(yīng)的數(shù);若不存在,說明理由;
BC+AB?若存在,求出點M對應(yīng)的數(shù);若不存在,說明理由;
(3)如圖②,若N點是B點右側(cè)一點,NA的中點為Q,P為NB的三等分點且靠近于B點,當(dāng)N在B的右側(cè)運動時,請直接判斷![]() 的值是不變的還是變的,如果不變請直接寫出其值,如果是變的請說明理由.
的值是不變的還是變的,如果不變請直接寫出其值,如果是變的請說明理由.
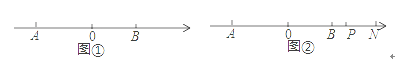
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3.點D是BC邊上的一動點(不與點B、C重合),過點D作DE⊥BC交AB于點E,將∠B沿直線DE翻折,點B落在射線BC上的點F處.當(dāng)△AEF為直角三角形時,BD的長為 . 
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知△ABC的周長是20,三邊分別為a,b,c.
(1)若b是最大邊,求b的取值范圍;
(2)若△ABC是三邊均不相等的三角形,b是最大邊,c是最小邊,且b=3c,a,b,c均為整數(shù),求△ABC的三邊長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】閱讀下面材料:
小明想探究函數(shù)![]() 的性質(zhì),他借助計算器求出了y與x的幾組對應(yīng)值,并在平面直角坐標系中畫出了函數(shù)圖象:
的性質(zhì),他借助計算器求出了y與x的幾組對應(yīng)值,并在平面直角坐標系中畫出了函數(shù)圖象:
x | … | -3 | -2 | -1 | 1 | 2 | 3 | … |
y | … | 2.83 | 1.73 | 0 | 0 | 1.73 | 2.83 | … |

小聰看了一眼就說:“你畫的圖象肯定是錯誤的.”
請回答:小聰判斷的理由是_____________.請寫出函數(shù)![]() 的一條性質(zhì):_____________.
的一條性質(zhì):_____________.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com