【題目】如圖，點A，B，C為平面內不在同一直線上的三點．點D為平面內一個動點．線段AB，BC，CD，DA的中點分別為M，N，P，Q．在點D的運動過程中，有下列結論：①存在無數個中點四邊形MNPQ是平行四邊形；②存在無數個中點四邊形MNPQ是菱形；③存在無數個中點四邊形MNPQ是矩形；④存在兩個中點四邊形MNPQ是正方形．所有正確結論的序號是_____．
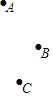
【答案】①②③④．
【解析】
連接AC、BD，根據三角形中位線定理得到PQ∥AC，PQ=
AC，MN∥AC，MN=AC，根據平行四邊形、矩形、菱形、正方形的判定定理判斷即可．
①當AC與BD不平行時，中點四邊形MNPQ是平行四邊形；
故存在無數個中點四邊形MNPQ是平行四邊形；
②當AC與BD相等且不平行時，中點四邊形MNPQ是菱形；
故存在無數個中點四邊形MNPQ是菱形；
③當AC與BD互相垂直（B，D不重合）時，中點四邊形MNPQ是矩形；
故存在無數個中點四邊形MNPQ是矩形；
④如圖所示，當AC與BD相等且互相垂直時，中點四邊形MNPQ是正方形．
故存在兩個中點四邊形MNPQ是正方形．
故答案為：①②③④．
科目：初中數學 來源： 題型：
【題目】某校在開展讀書交流活動中，全體師生積極捐書，為了解所捐書籍的種類，對部分書籍進行了抽樣調查，張老師根據調查數據繪制了如下不完整的統計圖．
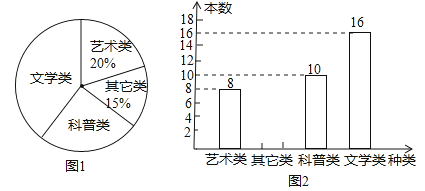
請根據統計圖回答下列問題：
（1）本次抽樣調查的書籍有多少本？
（2）試求圖1中表示文學類書籍的扇形圓心角的度數，并補全條形統計圖．
（3）本次活動師生共捐書
本，請估計有多少本科普類書籍？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】對于平面直角坐標系xOy中的任意點
，如果滿足
(x≥0，a為常數)，那么我們稱這樣的點叫做“特征點”．
（1）當2≤a≤3時，
①在點
中，滿足此條件的特征點為__________________；
②⊙W的圓心為
，半徑為1，如果⊙W上始終存在滿足條件的特征點，請畫出示意圖，并直接寫出m的取值范圍；
（2）已知函數
，請利用特征點求出該函數的最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如果
的兩個端點
分別在
的兩邊上(不與點
重合)，并且除端點外的所有點都在的內部，則稱是的“連角弧”．
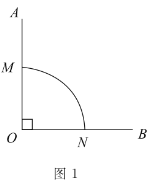
(1)圖1中，是直角，是以為圓心，半徑為1的“連角弧”．
①圖中的長是______，并在圖中再作一條以
為端點、長度相同的“連角弧”；
②以為端點，弧長最長的“連角弧”的長度是_______．
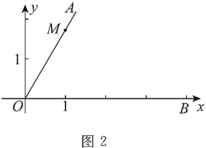
(2)如圖2，在平面直角坐標系
中，點
，點
在
軸正半軸上，若是半圓，也是的“連角弧”，求
的取值范圍．
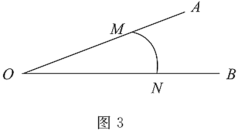
(3)如圖3，已知點分別在射線
上，
是的“連角弧”，且所在圓的半徑為
，直接寫出的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：在平面直角坐標系
中，對于任意的實數
，直線
都經過平面內一個定點
．
（1）求點的坐標．
（2）反比例函數
的圖象與直線交于點和另外一點
①求
的值；
②當
時，求
的取值范圍
查看答案和解析>>
科目：初中數學 來源： 題型：
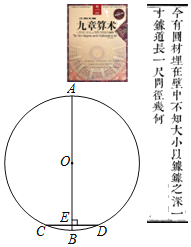
【題目】《九章算術》是中國傳統數學重要的著作之一，奠定了中國傳統數學的基本框架．其中卷九中記載了一個問題：“今有圓材，埋在壁中，不知大小，以鋸鋸之，深一寸，鋸道長一尺，問徑幾何？”其意思是：如圖，AB為⊙O的直徑，弦CD⊥AB于點E，BE＝1寸，CD＝1尺，那么直徑AB的長為多少寸？（注：1尺＝10寸）根據題意，該圓的直徑為_____寸．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，線段AB＝5cm，∠BAM＝90°，P是
與∠BAM所圍成的圖形的外部的一定點，C是上一動點，連接PC交弦AB于點D．設A，D兩點間的距離為xcm，P，D兩點間的距離為y1cm，P，C兩點間的距離為y2cm．小騰根據學習函數的經驗，分別對函數y1，y2隨自變量x的變化而變化的規律進行了探究．
下面是小騰的探究過程，請補充完整：
按照表中自變量x的值進行取點、畫圖、測量，分別得到了y1，y2與x的幾組對應值：
x/cm | 0.00 | 1.00 | 1.56 | 1.98 | 2.50 | 3.38 | 4.00 | 4.40 | 5.00 |
y1/cm | 2.75 | 3.24 | 3.61 | 3.92 | 4.32 | 5.06 | 5.60 | 5.95 | 6.50 |
y2/cm | 2.75 | 4.74 | 5.34 | 5.66 | 5.94 | 6.24 | 6.37 | 6.43 | 6.50 |
（1）在同一平面直角坐標系xOy中，畫出各組數值所對應的點（x，y1），（x，y2），并畫出函數y1，y2的圖象；
（2）連接BP，結合函數圖象，解決問題：當△BDP為等腰三角形時，x的值約為_____cm（結果保留一位小數）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知二次函數y＝﹣x2+bx+c的圖象經過點A（3，1），點B（0，4）．
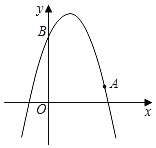
（1）求該二次函數的表達式及頂點坐標；
（2）點C（m，n）在該二次函數圖象上．
①當m＝﹣1時，求n的值；
②當m≤x≤3時，n最大值為5，最小值為1，請根據圖象直接寫出m的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
