
【題目】在△ABC中,AB=CB,∠ABC=90°,E為CB延長線上一點,點F在AB上,且AE=CF.

(1)求證:Rt△ABE≌Rt△CBF;
(2)若∠CAE=60°,求∠ACF的度數.
【答案】(1)Rt△ABE≌Rt△CBF;(2)∠ACF=30°.
【解析】
試題(1)在Rt△ABE和Rt△CBF中,由于AB=CB,AE=CF,利用HL可證Rt△ABE≌Rt△CBF;
(2)由等腰直角三角形的性質易求∠BAE=∠CAE﹣∠CAB=15°.利用(1)中全等三角形的對應角相等得到∠BAE=∠BCF=15°,則∠ACF=∠ACB﹣∠BCF=30°.即∠ACF的度數是30°.
(1)證明:在Rt△ABE和Rt△CBF中,
∵![]() ,
,
∴Rt△ABE≌Rt△CBF(HL);
(2)如圖,∵在△ABC中,AB=CB,∠ABC=90°,
∴∠ACB=∠CAB=45°,
∴∠BAE=∠CAE﹣∠CAB=15°.
又由(1)知,Rt△ABE≌Rt△CBF,
∴∠BAE=∠BCF=15°,
∴∠ACF=∠ACB﹣∠BCF=30°.即∠ACF的度數是30°.


科目:初中數學 來源: 題型:
【題目】小明、小華在一棟電梯樓前感慨樓房真高.小明說:“這樓起碼20層!”小華卻不以為然:“20層?我看沒有,數數就知道了!”小明說:“有本事,你不用數也能明白!”小華想了想說:“沒問題!讓我們來量一量吧!”小明、小華在樓體兩側各選A、B兩點,測量數據如圖,其中矩形CDEF表示樓體,AB=150米,CD=10米,∠A=30°,∠B=45°,(A、C、D、B四點在同一直線上)問:

(1)樓高多少米?
(2)若每層樓按3米計算,你支持小明還是小華的觀點呢?請說明理由.(參考數據:![]() ≈1.73,
≈1.73,![]() ≈1.41,
≈1.41,![]() ≈2.24)
≈2.24)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的不等式組 有且只有四個整數解,又關于x的分式方程
有且只有四個整數解,又關于x的分式方程![]() ﹣2=
﹣2=![]() 有正數解,則滿足條件的整數k的和為( )
有正數解,則滿足條件的整數k的和為( )
A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知OD=OC,添加下列四個條件中的一個,仍不能得到△ODA與△OCB全等的是( )

A.∠D=∠CB.OA=OBC.BD=ACD.AD=BC
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,點D是線段AB的中點,DC⊥BC,作∠EAB=∠B,DE∥BC,連接CE.若![]() ,設△BCD的面積為S,則用S表示△ACE的面積正確的是( )
,設△BCD的面積為S,則用S表示△ACE的面積正確的是( )

A.![]() B.3S
B.3S
C.4SD.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,AB=10cm,BC=6cm,若動點P從點C開始出發,按C→A→B→C的路徑運動,且速度為每秒2cm,設出發的時間為t秒.
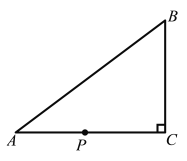
(1)填空:AC= cm;
(2)若點P恰好在∠ABC的角平分線上,求t的值;
(3)當t為何值時,△BPC為等腰三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD的對角線AC、BD相交于點O,AE平分∠BAD,分別交BC、BD于點E、P,連接OE,∠ADC=60°,AB=![]() BC=1,則下列結論:
BC=1,則下列結論:
①∠CAD=30°②BD=![]() ③S平行四邊形ABCD=ABAC④OE=
③S平行四邊形ABCD=ABAC④OE=![]() AD⑤S△APO=
AD⑤S△APO=![]() ,正確的個數是( )
,正確的個數是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com