【題目】已知函數
是關于
的二次函數，求：
求滿足條件的
值；
當拋物線開口向下時，請寫出此時拋物線的頂點坐標；
為何值時，拋物線有最小值？最小值是多少？當為何值時，
隨的增大而增大？
科目：初中數學 來源： 題型：
【題目】我市某企業接到一批產品的生產任務，按要求必須在14天內完成．已知每件產品的出廠價為60元．工人甲第x天生產的產品數量為y件，y與x滿足如下關系：
(1)工人甲第幾天生產的產品數量為70件？
(2)設第x天生產的產品成本為P元/件，P與
的函數圖象如圖．工人甲第x天創造的利潤為W元，求W與x的函數關系式，并求出第幾天時利潤最大，最大利潤是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】隨著地鐵和共享單車的發展，“地鐵
單車”已成為很多市民出行的選擇
張老師從學校站出發，先乘坐地鐵到某一站出地鐵，再騎共享單車回家，設他出地鐵的站點與學校距離為
單位：千米
，乘坐地鐵的時間為
單位分鐘，經測量，得到如下數據：
地鐵站 | A | B | C | D |
| E |
| 6 |
| 10 | |
| 15 |
| 9 | 12 | a | 20 |
| b |
根據表中數據的規律，直接寫出表格中a、b的值和
關于x的函數表達式；
張老師騎單車的時間
單位：分鐘也受x的影響，其關系可以用
米描述，
若張老師出地鐵的站點與學校距離為14千米，請求出張老師從學校回到家所需的時間；
若張老師準備在離家較近的A，B，C，D，E中的某一站出地鐵，請問：張老師應選擇在哪一站出地鐵，才能使他從學校回到家所需的時間最短？并求出最短時間．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，將ABCD的AD邊延長至點E，使DE＝
AD，連接CE，F是BC邊的中點，連接FD．
(1)求證：四邊形CEDF是平行四邊形；
(2)若AB＝3，AD＝4，∠A＝60°，求CE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：直線y＝
x+3與x軸、y軸分別相于點A和點B，點C在線段AO上．
將△CBO沿BC折疊后，點O恰好落在AB邊上點D處
（1）求直線BC的解析式；
（2）求點D的坐標；
（3）P為平面內一動點，且以A、B、C、P為頂點的四邊形為平行四邊形，直接寫出點P坐標 ．
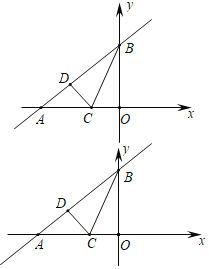
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀理解題
（1）閱讀理解：如圖①，等邊
內有一點
，若點到頂點
，
，
的距離分別為3，4，5，求
的大小.
思路點撥：考慮到
，
，
不在一個三角形中，采用轉化與化歸的數學思想，可以將
繞頂點逆時針旋轉
到
處，此時
，這樣，就可以利用全等三角形知識，結合已知條件，將三條線段的長度轉化到一個三角形中，從而求出的度數.請你寫出完整的解題過程.
（2）變式拓展：請你利用第（1）題的解答思想方法，解答下面問題：
已知如圖②，中，
，
，
、
為
上的點且
，
，
，求
的大小.
（3）能力提升：如圖③，在
中，
，
，
，點
為內一點，連接
，
，
，且
，請直接寫出
的值，即
______.
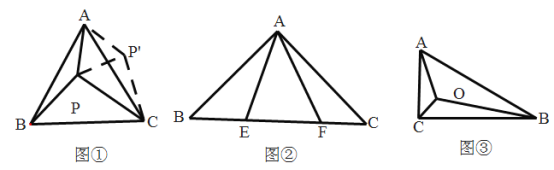
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知△ABC內接于⊙O，過點A作直線EF．
（1）如圖①，AB是直徑，要使EF是⊙O的切線，還須添加一個條件是（只需寫出三種情況）．
（ī） （īī） （īīī）
（2）如圖（2），若AB為非直徑的弦，∠CAE＝∠B，則EF是⊙O的切線嗎？為什么？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
