Question

【題目】平面直角坐標系中，矩形的頂點的坐標分別為，，，且滿足；

（1）矩形的頂點的坐標是（ ， ）．

（2）若是中點，沿折疊矩形使點落在處，折痕為，連并延長交于，求直線的解析式．

（3）將（2）中直線向左平移個單位交軸于，為第二象限內的一個動點，且，求的最大值．

Answer 1

【答案】（1）（6，8）；（2）；（3）

【解析】

（1）將整理即為，根據平方和二次根式的性質可得：，，求解即可得到a、b的值，即可求出B點坐標；

（2）作輔助線過點E作x軸的平行線交y軸于點G、交AB于點H，先證明，設：，，得，即：，

解出m、n的值，即求出E點坐標，將點C、E的坐標代入一次函數表達式求解即可；
（3）過點N、O、M作圓R（R為圓心），連接RM、RO，當F、R、N三點共線時，FN最大，即可求解．

(1)將整理即為，

∵根據平方和二次根式的性質可得：，，

解得：，，

∴B點坐標為：（6，8）；
(2)如圖過點E作x軸的平行線交y軸于點G、交AB于點H，

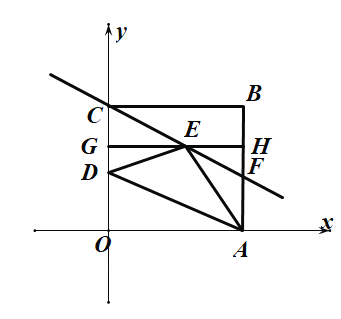
設：，，

∵，，

∴，

∴，

∴，即：，

解得：，，

∴E點坐標為，

設直線CE的解析式為：，將點C、E的坐標代入一次函數表達式并解得：

直線CE的表達式為：；

(3) 中，當x=6時，y=4，故點F（6，4），

直線CE向左平移一個單位后的表達式為：，可求出M點坐標為：，

如圖過點N、O、M作圓R（R為圓心），連接RM、RO，

當F、R、N三點共線時，FN最大，

∵，

∴，則為等腰直角三角形，

∴點R的坐標為，

∵為等腰直角三角形，

∴，

∴由點F、R的坐標得， ，

FN的最大值=．