
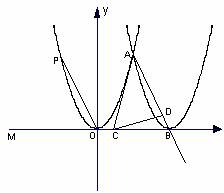
如圖,點P(-m,m2)拋物線:y = x2上一點,將拋物線E沿x軸正方向平移2m個單位得到拋物線F,拋物線F的頂點為B,拋物線F交拋物線E于點A,點C是x軸上點B左側一動點,點D是射線AB上一點,且∠ACD = ∠POM.問△ACD能否為等腰三角形?
若能,求點C的坐標;若不能,請說明理由.
說明:⑴如果你反復探索,沒有解決問題,請寫出探索過程(要求至少寫3步);⑵在你完成⑴之后,可以從①、②中選取一個條件,完成解答
①m = 1;②m = 2.
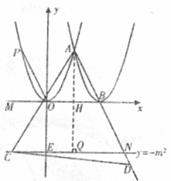
附加題:如下圖,若將上題“點C是x軸上點B左側一動點”改為“點C是直線y =-m2上點N左側一動點”,其他條件不變,探究上題中的問題.
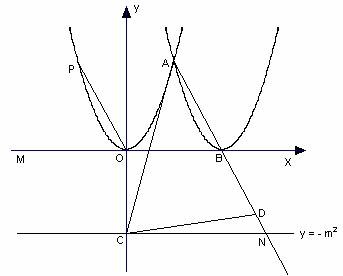
解:![]() ACD能為等腰三角形
ACD能為等腰三角形
由平移的性質可得,A點坐標為(![]() ),B點坐標(
),B點坐標(![]() )
)
設C點坐標為(![]() ),過A點作AH
),過A點作AH![]()
![]() 軸,垂足為H,連結AO,
軸,垂足為H,連結AO,
![]() A點坐標為(
A點坐標為(![]() ),
),![]() H點坐標為(m,0),AH=
H點坐標為(m,0),AH=![]()
![]() B點坐標為(
B點坐標為(![]() ),
),![]() OH=BH=m
OH=BH=m
![]() AB=AO,
AB=AO,![]()
![]() ABC=
ABC=![]() AOB,由已知可得,AB//OP,
AOB,由已知可得,AB//OP, ![]()
![]() ABC=
ABC=![]() POM
POM
又![]()
![]() ACD=
ACD=![]() POM,
POM, ![]()
![]() ACD=
ACD=![]() ABC=
ABC=![]() AOB
AOB
若![]() ACD為等腰三角形,則AC=AD,或CD=CA,或DA=DC
ACD為等腰三角形,則AC=AD,或CD=CA,或DA=DC
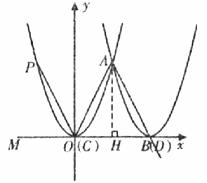
當AC=AD時,
如下圖,![]() AC=AD,
AC=AD,![]()
![]() ACD=
ACD=![]() ADC
ADC
![]()
![]() ADC=
ADC=![]() ACD=
ACD=![]() ABC
ABC![]() 點D與點B重合,點C與點O重合,
點D與點B重合,點C與點O重合,
![]() C點坐標為(0,0)
C點坐標為(0,0)
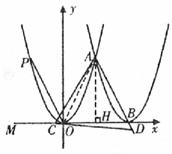
當CD=CA時,
方法一:
如下圖,![]() CD=CA,
CD=CA,![]()
![]() CAD=
CAD=![]() CDA,
CDA,![]()
![]() ABC=
ABC=![]() AOB,
AOB,
![]()
![]() CBD=
CBD=![]() AOC
AOC
![]()
![]() ACD=
ACD=![]() ABC,又
ABC,又![]()
![]() ABC=
ABC=![]() BCD+
BCD+![]() ADC,
ADC,
![]() ACD=
ACD=![]() BCD+
BCD+![]() ACB,
ACB,
![]()
![]() ADC=
ADC=![]() ACB,
ACB, ![]()
![]() BCD≌
BCD≌![]() OAC,
OAC,![]() BC=OA
BC=OA
在Rt![]() AOH中,OA2=OH2+AH2=m2+(m2)2,
AOH中,OA2=OH2+AH2=m2+(m2)2, ![]() BC=OA=
BC=OA=![]()
![]() OC=BC-OB=
OC=BC-OB=![]()
![]() C點坐標為(2m-
C點坐標為(2m-![]() ,0)
,0)
方法二:
如上圖,![]() CA=CD,
CA=CD,![]()
![]() CAD=
CAD=![]() CDA
CDA
又![]()
![]() ACD=
ACD=![]() ABC,
ABC, ![]() CAB=
CAB=![]() DAC,
DAC,
![]()
![]() ACB∽
ACB∽![]() ADC,
ADC,![]()
![]() ACB=
ACB=![]() CDA,
CDA,![]()
![]() CAD=
CAD=![]() ACB,
ACB,![]() BC=AB
BC=AB
![]() BC=OA
BC=OA
余下部分同方法一
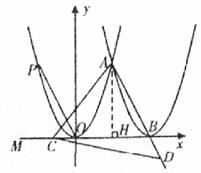
當DA=CD時,
如下圖,![]() DA=DC,
DA=DC,![]()
![]() DAC=
DAC=![]() ACD
ACD
![]()
![]() ACD=
ACD=![]() ABC,
ABC,![]()
![]() DAC=
DAC=![]() ABC,
ABC,![]() AC=BC
AC=BC
![]() BC=
BC=![]() ,
,![]() AC=
AC=![]()
在Rt![]() ACH中,AC2=AH2+CH2
ACH中,AC2=AH2+CH2
![]() (
(![]() )2=
)2=![]()
![]()
![]()
![]() C點坐標為(
C點坐標為(![]() ,0)
,0)
探索過程一:
由已知可得,AB//OP,![]()
![]() ABC=
ABC=![]() POM
POM
![]()
![]() ACD=
ACD=![]() POM,
POM,![]()
![]() ACD=
ACD=![]() POM=
POM=![]() ABC
ABC
探索過程二:
若![]() ACD為等腰三角形,則有三種可能,即AC=AD,或CD=CA,或DA=DC
ACD為等腰三角形,則有三種可能,即AC=AD,或CD=CA,或DA=DC
當AC=AD時,![]()
![]() ACD=
ACD=![]() ADC
ADC
選擇條件![]()
當m=1時,P點坐標為(-1,1),由平移性質可得,A點坐標為(1,1),
B點坐標為(2,0)
過A點作AH![]() x軸,垂足為H,連結AO,
x軸,垂足為H,連結AO,![]() H點坐標為(1,0),AH=1,OH=BH=1,
H點坐標為(1,0),AH=1,OH=BH=1,![]() AB=AO,
AB=AO,
![]()
![]() ABC=
ABC=![]() AOB=45
AOB=45![]() ,
,![]() OAB=90
OAB=90![]()
由已知可得,OP//AB,![]()
![]() ABC=
ABC=![]() POM
POM
又![]()
![]() ACD=
ACD=![]() POM,
POM, ![]()
![]() ACD=
ACD=![]() ABC=
ABC=![]() AOB=45
AOB=45![]()
若![]() ACD為等腰三角形,則有三種可能,即AC=AD,或CD=CA,或DA=DC
ACD為等腰三角形,則有三種可能,即AC=AD,或CD=CA,或DA=DC
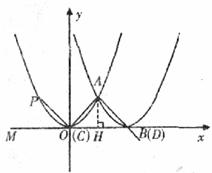
當AC=AD時,
如下圖,![]() AC=AD,
AC=AD,![]()
![]() ACD=
ACD=![]() ADC
ADC
![]()
![]() ACD=
ACD=![]() ABC,
ABC,![]()
![]() ABC=
ABC=![]() ADC=
ADC=![]() AOB,
AOB,
![]() 點D與點B重合,點C與點O重合,
點D與點B重合,點C與點O重合,![]() C點坐標為(0,0)
C點坐標為(0,0)
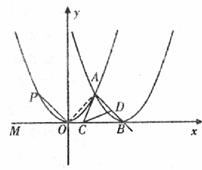
當CA=CD時,
方法一:
如下圖,![]() CA=CD,
CA=CD,![]()
![]() CAD=
CAD=![]() CDA
CDA
![]()
![]() ACB=
ACB=![]() AOB+
AOB+![]() OAC,
OAC,![]()
![]() ACD+
ACD+![]() DCB=
DCB=![]() AOB+
AOB+![]() OAC,
OAC,
![]()
![]() DCB=
DCB=![]() OAC
OAC
又![]()
![]() AOB=
AOB=![]() ABC,
ABC,![]()
![]() BCD≌
BCD≌![]() OAC,
OAC,![]() BC=OA
BC=OA
在Rt![]() AOB中,OB2=OA2+AB2=2OA2,
AOB中,OB2=OA2+AB2=2OA2,
![]() 4=2OA2,
4=2OA2,![]() OA=
OA=![]()
![]() OC=OB-BC=OB-OA=2-
OC=OB-BC=OB-OA=2-![]() ,
,
![]() C點坐標為(2-
C點坐標為(2-![]() ,0)
,0)
方法二:
如上圖,![]() CA=CD,
CA=CD,![]()
![]() CAD=
CAD=![]() CDA
CDA
又![]()
![]() ACD=
ACD=![]() ABC,
ABC,![]() CAD=
CAD=![]() BAC,
BAC,
![]() ACD∽
ACD∽![]() ABC,
ABC,![]()
![]() CDA=
CDA=![]() ACB
ACB
![]()
![]() CAD=
CAD=![]() ACB,
ACB,![]() AB=BC
AB=BC
在Rt![]() AOB中,OB2=OA2+AB2=2AB2
AOB中,OB2=OA2+AB2=2AB2
![]() 4=2AB2,
4=2AB2, ![]() AB=
AB=![]()
![]() BC=
BC=![]() ,
,![]() OC=OB-BC=2-
OC=OB-BC=2-![]()
![]() C點坐標為(2-
C點坐標為(2-![]() ,0)
,0)
當DA=DC時,
如下圖,![]() DA=DC,
DA=DC,![]()
![]() ACD=
ACD=![]() DAC
DAC
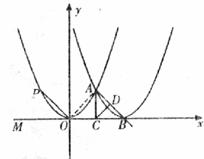
![]() 平分
平分![]() OAB,又
OAB,又![]() AO=AB,
AO=AB,
![]() C是OB中點,
C是OB中點,
![]() C點坐標為(1,0)
C點坐標為(1,0)
選擇條件![]()
當m=2時,P點坐標為(-2,4),由平移的性質得,A點坐標為(2,4),B點坐標為
(4,0)
連結OA,過A點作AH![]()
![]() 軸,垂足為H,
軸,垂足為H,
![]() H點坐標為(2,0),AH=4,OH=BH=2,
H點坐標為(2,0),AH=4,OH=BH=2,
![]() AB=AO,
AB=AO,![]()
![]() ABC=
ABC=![]() AOB
AOB
由已知可得,OP//AB,![]()
![]() ABC=
ABC=![]() POM,
POM,
又![]()
![]() ACD=
ACD=![]() POM,
POM,![]()
![]() ACD=
ACD=![]() ABC=
ABC=![]() AOB
AOB
若![]() ACD為等腰三角形,則有三種可能,即AC=AD,或CD=CA,或DA=DC
ACD為等腰三角形,則有三種可能,即AC=AD,或CD=CA,或DA=DC
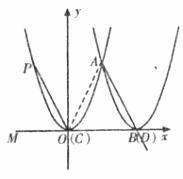
當AC=AD時,
如下圖,![]() AC=AD,
AC=AD,![]()
![]() ACD=
ACD=![]() ADC
ADC
又![]()
![]() ACD=
ACD=![]() ABC=
ABC=![]() AOB
AOB
![]()
![]() ACD=
ACD=![]() ABC=
ABC=![]() AOB=
AOB=![]() ADC
ADC
![]() 點D與點B重合,點C與點D重合
點D與點B重合,點C與點D重合
![]() C點坐標為(0,0)
C點坐標為(0,0)
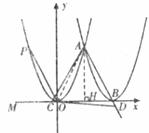
當CA=CD時,
方法一:
如下圖,![]() CA=CD,
CA=CD,![]()
![]() CAD=
CAD=![]() CDA
CDA
![]()
![]() ABC=
ABC=![]() ADC+
ADC+![]() BCD
BCD
又![]()
![]() ACD=
ACD=![]() ACD+
ACD+![]() BCD,
BCD,![]() ACD=
ACD=![]() ABC,
ABC,
![]()
![]() ADC=
ADC=![]() ACB
ACB
又![]()
![]() ABC=
ABC=![]() AOB,
AOB,![]()
![]() CBD=
CBD=![]() AOC,
AOC,
![]()
![]() CBD≌
CBD≌![]() AOC,
AOC,![]() BC=OA
BC=OA
在Rt![]() AOH中,OA2=AH2+OH2=42+22=20,
AOH中,OA2=AH2+OH2=42+22=20,![]() BC=OA=
BC=OA=![]()
![]() OC=BC-OB=
OC=BC-OB=![]() ,
,![]() C點坐標為(
C點坐標為(![]() ,0)
,0)
方法二:
如上圖,![]() CA=CD,
CA=CD,![]()
![]() CAD=
CAD=![]() CDA,
CDA,![]()
![]() ACD=
ACD=![]() ABC,
ABC,
又![]()
![]() CAD=
CAD=![]() BAC,
BAC,
![]()
![]() ACD≌
ACD≌![]() ABC,
ABC,![]()
![]() CDA=
CDA=![]() ACB,
ACB,![]()
![]() CAD=
CAD=![]() ACB
ACB
![]() AB=BC
AB=BC
在Rt![]() ABH中,AB2= AH2+BH2=42+22=20
ABH中,AB2= AH2+BH2=42+22=20
![]() BC=AB=
BC=AB=![]()
![]() OC=BC-OB=
OC=BC-OB=![]() -4,
-4,![]() C點坐標為(4-
C點坐標為(4-![]() ,0)
,0)
當DA=DC時,
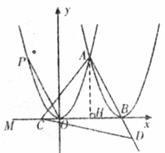
如上圖,![]() DA=DC.
DA=DC. ![]()
![]() DAC=
DAC=![]() ACD
ACD
![]()
![]() ACD=
ACD=![]() ABC,
ABC,![]()
![]() DAC=
DAC=![]() ABC
ABC
![]() AC=BC
AC=BC
在Rt![]() ACH中,AC=AH2+CH2
ACH中,AC=AH2+CH2
![]() (4-
(4-![]() )2=42+(2-
)2=42+(2-![]() )2,
)2, ![]() x=-1
x=-1
![]() C點坐標為(-1,0)
C點坐標為(-1,0)
附加題:
解:![]() ACD能為等腰三角形,
ACD能為等腰三角形,
設C點坐標為(x,-m2)
由上題知,H點坐標為(m,0),AH=m2
設AH延長線交y=-m2于點Q,![]() Q點坐標為(m,- m2),AQ=2 m2,
Q點坐標為(m,- m2),AQ=2 m2,
![]() AH=HQ,
AH=HQ, ![]() QN=2BH=2m,
QN=2BH=2m,
![]() N點坐標為(3m, m2)
N點坐標為(3m, m2)
由題意知,OB//CN,![]()
![]() ABO=
ABO=![]() ANC
ANC
由上題知,![]() POM=
POM=![]() ABO,
ABO,
又![]()
![]() ACD=
ACD=![]() POM,
POM,![]()
![]() ACD=
ACD=![]() ANC
ANC
若![]() ACD為等腰三角形,則AC=AD,或CD=CA,或DA=DC,
ACD為等腰三角形,則AC=AD,或CD=CA,或DA=DC,
當AC=AD時,
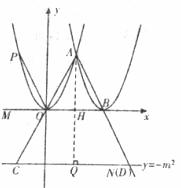
如上圖,![]() AC=AD,
AC=AD,![]()
![]() ACD=
ACD=![]() ADC
ADC
![]()
![]() ADC=
ADC=![]() ACD=
ACD=![]() ANC,
ANC,![]() 點D與點N重合,
點D與點N重合,
![]() CQ=QN,
CQ=QN,![]() CQ=2m,
CQ=2m,
![]() C點是坐標為(-m,- m2)
C點是坐標為(-m,- m2)
當CD=CD時,
如下圖,![]() CD=CA,
CD=CA,![]()
![]() ADC=
ADC=![]() CAD
CAD
![]()
![]() ACD=
ACD=![]() ANC,
ANC,![]() CAD=
CAD=![]() NAC,
NAC,
![]()
![]() ACN∽
ACN∽![]() ADC,
ADC,![]()
![]() ACN=
ACN=![]() ADC,
ADC,
![]()
![]() CAD=
CAD=![]() ACN,
ACN,![]() CN=AN
CN=AN
在Rt![]() ANQ中,
ANQ中,
AN2=AQ2+NQ2=(2m2)2+(2m)2=4m4+4m2,
![]() CN=AN=
CN=AN=![]()
![]() CE=CN-EN=
CE=CN-EN=![]() -3m
-3m
![]() C點坐標為(3m-
C點坐標為(3m-![]() ,-m2)
,-m2)
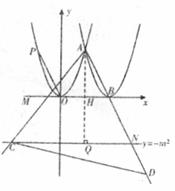
當DA=DC時
如下圖,![]() DA=DC,
DA=DC,![]()
![]() DAC=
DAC=![]() ACD
ACD
![]()
![]() ACD=
ACD=![]() ANC,
ANC,![]()
![]() ANC=
ANC=![]() DAC,
DAC,![]() CN=AC
CN=AC
在Rt![]() ACQ中,AC2=AQ2+CQ2
ACQ中,AC2=AQ2+CQ2
![]() (3m-x)2=(2m2)2+(m-x)2,
(3m-x)2=(2m2)2+(m-x)2, ![]() x=2m-m3,
x=2m-m3,
![]() C點坐標為(2m-m3,-m2)
C點坐標為(2m-m3,-m2)


科目:初中數學 來源: 題型:
 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,點A的坐標為(2
如圖,點A的坐標為(2| 2 |
| A、(0,0) | ||||||||
B、(
| ||||||||
| C、(1,1) | ||||||||
D、(
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com